Kinematics Overview
로보틱스 관련 용어
•
path: 로봇이 움직이고 싶어하는 점들의 집합
•
kinematic constraints: 로봇의 관절마다 정해져 있는 기구적 제한조건
•
dynamic constraints: 관절의 구동계는 최대 토크, 최대 속도, 가속도 조건이 있으며 이를 dynamic constraints라 함
•
Trajectory Planning: 우리가 원하는 path에 두 조건 (kinematic constraints, dynamic constraints)을 만족하는 (시간 기준의)position, velocity, acceleration을 찾는 문제
Inverse Kinematics (IK)
로봇의 hand 쪽을 end-effector라 하고 이동할 위치에 해당하는 의 공간을 task(cartesian) space라 하고 각도 joint의 공간 의 집합을 joint space라 한다.
•
Forward Kinematics : joint space → task space ()
•
Inverse Kinematics : task space → joint space ()
IK Solvers
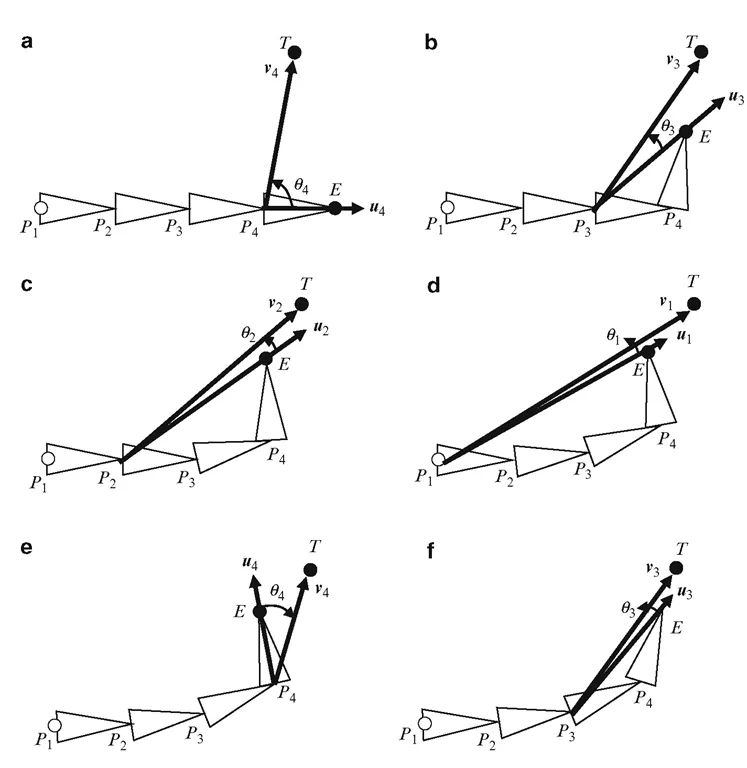
Cyclic coordinate Descent (CCD)
1.
joint 마다 순회하며 end effector와 target path 사이의 각도가 최소가 되도록 각도를 변환한다.
i.
타겟의 위치 , end effector와 (joint)의 사이각의 라 할 때, 의 각도가 0이 되도록 end effector를 이동한다.
ii.
end effector부터 base 까지 역순으로 i의 과정을 진행한다.
2.
만족스러울 때 까지 1번 과정을 반복한다.
관절각도는 타겟의 위치()와 두 관절 사이에서 생기는 위치 사이의 벡터 의 내적을 이용하여 구한다.
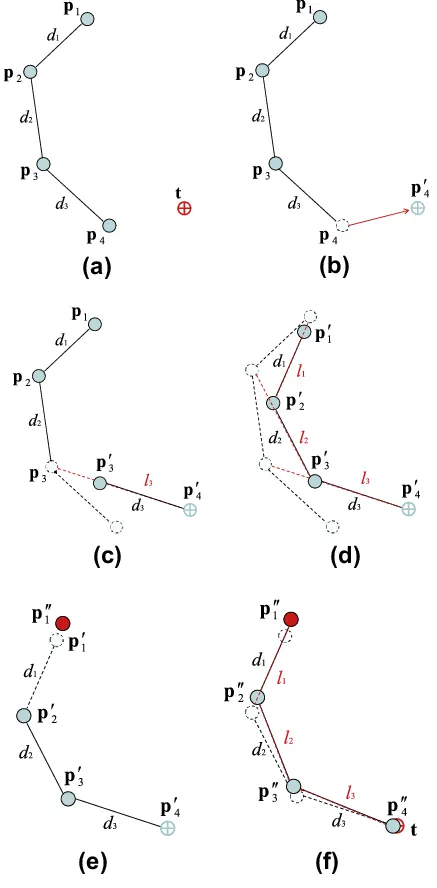
Forward And Backward Reaching Inverse Kinematics (FABIK)
1.
Forward
i.
(end effector)를 타겟의 위치()로 이동한다. 이동한 는 라 한다.
ii.
와 를 잇는 벡터 위에 로 부터 거리가 가 되는 위치 를 찾는다.
iii.
까지 위 두 과정을 진행한다.
2.
Backward
i.
Base joint 을 다시 원래의 위치로 옮긴다. 옮긴 의 새로운 위치는 이라 한다.
ii.
위 과정을 역순으로 (end effector)까지 진행한다.
3.
iteration
만족스러울 때 까지 위 1과 2 과정을 반복한다.