Search

Thin Plate Spline(TPS)

리뷰완료날짜
2024/03/19
리뷰어
카테고리
기타
출판
파일
깃헙주소
태그
TPS(Thin Plate Spline)는 스플라인 기반의 데이터 보간 방법으로, 이미지의 와핑문제를 해결하는데 주로 사용된다. 와핑문제는 컨트롤포인트의 이동과 주변점들의 스무스한 이동을 동시에 고려하는 문제로, 이를 해결하기 위해 RBF(Radial Basis Function Interpolation)와 같은 보간방식이 사용된다. TPS는 2차원 이상의 데이터에서도 스무스한 보간을 가능하게 하며, 국소적인 변화를 효과적으로 다룰 수 있다. TPS는 특히 버츄얼트라이온(virtual try-on) 분야에서 옷을 신체에 맞게 변형시키는 방법론에서 많이 활용된다.
스플라인(spline) 기반의 데이터 보간 방법으로 우리말로 박막스플라인이라고도 한다. 스플라인이랑 곡선들이 서로의 양 끝점에 연결된것을 말한다(참고로 서로 만나는 점을 노트(knot)라고 한다). TPS는 이미지의 와핑문제를 해결하기 위해 자주 활용된다. 본 페이지에서는 먼저 와핑문제가 무엇인지, 어떤식으로 해결을 하려하는지 설명한 후에 TPS방식을 소개하려고 한다.

와핑 문제란?

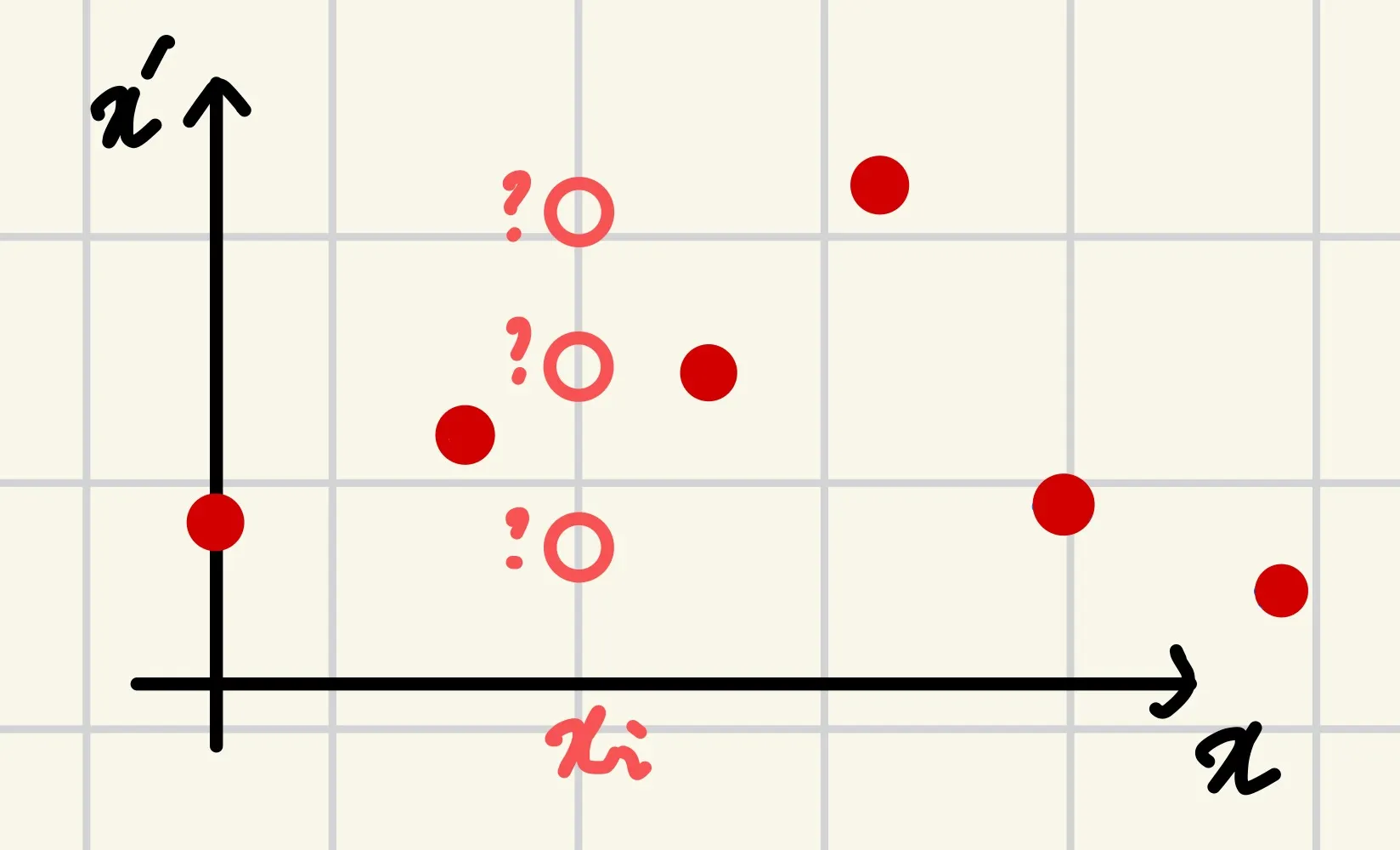
컨트롤 할 수 있는 점(컨트롤포인트;control points)들인 (xi,yi)(x_i,y_i)가 주어졌을 때 이 점을 (xi′,yi′)(x_{i}', y_{i}')로 옮기는 함수 ff가 있다고 하자(f:(x,y)↦(x′,y′)f:(x,y)\mapsto (x',y')). 이 과정에서 이동 변위를 (△xi,△yi)(\bigtriangleup x_i, \bigtriangleup y_i)라 하자. 와핑문제는 컨트롤포인트(xi,yi)(x_i,y_i)가 이동한 결과인 (xi+△xi,yi+△yi)(x_i+\bigtriangleup x_i, y_i+\bigtriangleup y_i)가 (xi′,yi′)(x_{i}', y_{i}')에 가장 근사한 값이 되면서도 컨트롤포인트의 주변점들은 스무스하게(smoothly)하게 이동할 수 있도록 하는 ff를 구하는 문제이다.
즉, (xi,yi)(x_i,y_i)와 (xi′,yi′)(x_{i}', y_{i}')를 매칭시키는 과정에서 (xi,yi)(x_i,y_i)의 주변점이 어디에 매칭이 되어야 하는것을 해결한다는 점에서 보간(interpolation)문제로 볼 수 있는것이다. 편의상 1차원(xi↦xi′x_i\mapsto x_i')으로 문제를 축소시키면 아래 그림과 같이 표현할 수 있다.
이를 해결하기 위한 보간방식 중 하나가 본 페이지에서 소개하는 TPS다.

Radial Basis Function Interpolation(RBF)

TPS를 설명하기 전에 TPS의 기본형인 RBF에 대해 먼저 설명하려고 한다. 우선 설명의 편의를 위해 앞서 표현한대로 1차원에 대해서만 우선적으로 논의하자.
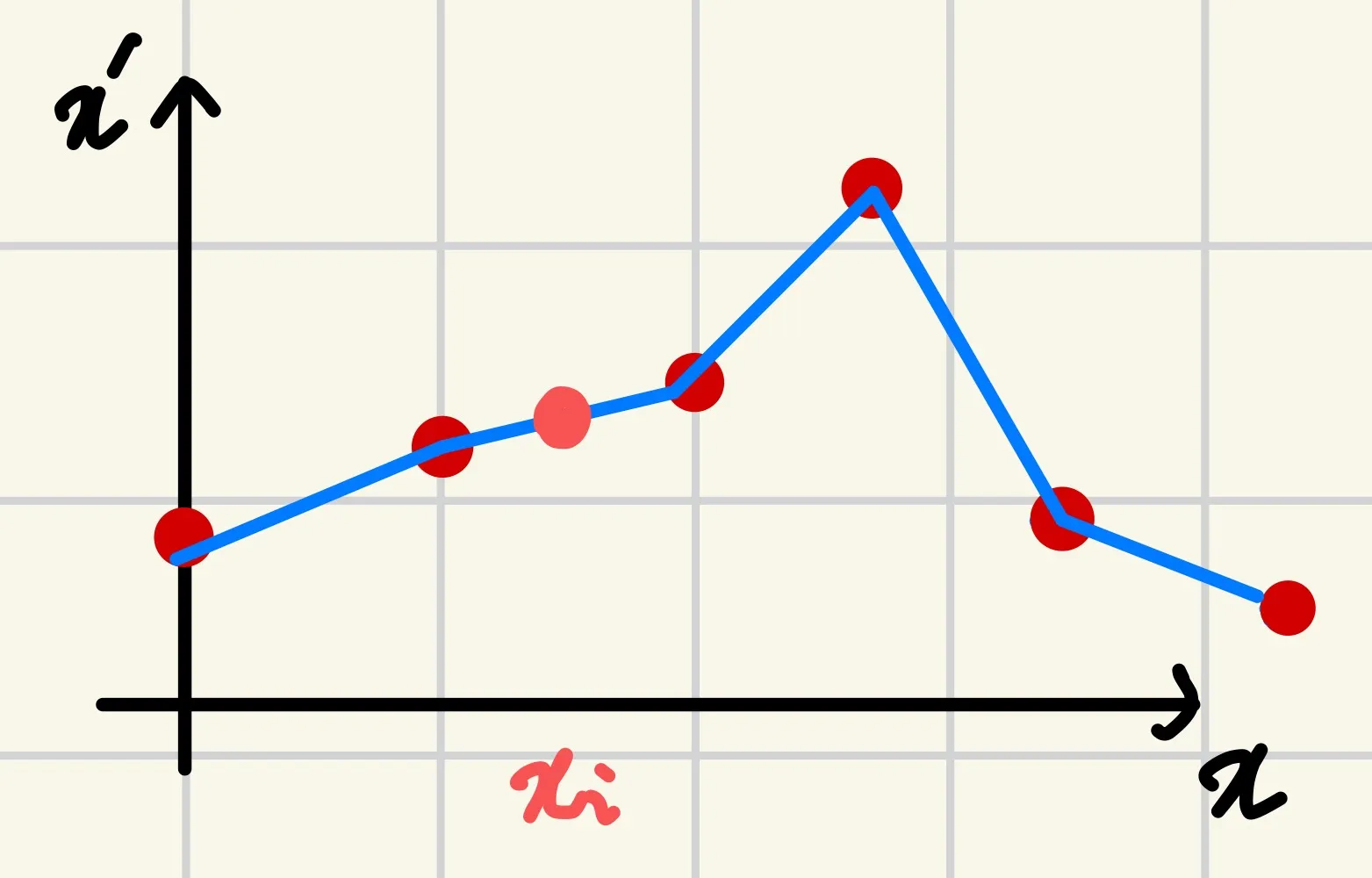
가장 직관적인 방법은 아래 그림과 같이 선형함수들의 조합으로 점들을 보간하는것이다.
image is modified from Khanh’s blog
그러나 우리가 구하려는 함수 ff는 스무스한 보간 함수(smooth interpolation function)인데 해당 방식은 스무스하지 않다. 이를 xix_i를 중심으로 하는 스무스커널(smooth kernel)을 통해 해결한 방식을 Radial Basis Function Interpolation(RBF)라 한다.
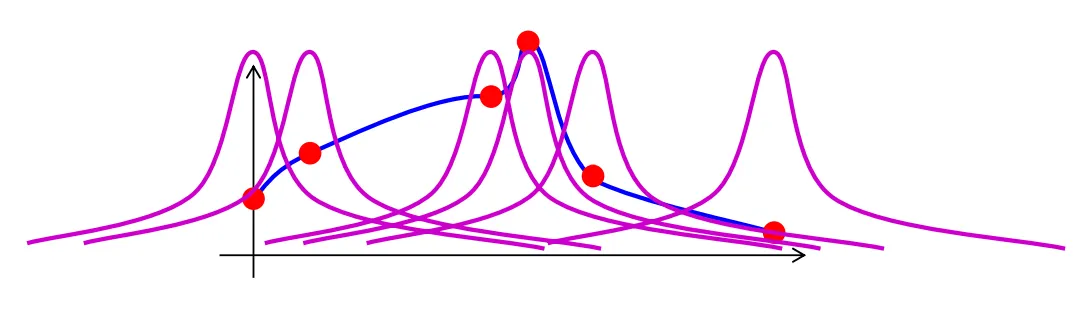
먼저 아래 그림과 같이 각 컨트롤포인트 xix_i에 자신을 중심으로 하는 스무스 커널 RR을 위치시킨다.
image is from Khanh’s blog
이후 각 점을 모든 커널에 넣었을 때 나오는 값들에 가중치를 곱하여 합한 값이 x′x'가 되도록 함수를 설계한다. 수식으로 표현하면 아래와 같다.
f(z)=∑iαiR(z;xi)f(z)=\sum_i \alpha_i R(z;x_i)
여기서 α\alpha는 각 커널의 가중치(weights)를 의미하며 f(xi)≒xi′f(x_i)\fallingdotseq x_i'가 되도록 α\alpha값을 찾아야 한다. 커널함수 R(z;xi)R(z;x_i)는 다양하게 선택이 가능하다.
결론적으로 해당 전 과정을 행렬식으로 표현하면 아래와 같다.
[xo′x1′x2′]=[R(x0;x0)R(x0;x1)R(x0;x2)R(x1;x0)R(x1;x1)R(x1;x2)R(x2;x0)R(x2;x1)R(x2;x2)]×[α0α1α2]\begin{bmatrix} x_o' \\ x_1' \\ x_2' \\ \end{bmatrix} = \begin{bmatrix} R(x_0;x_0) & R(x_0;x_1) & R(x_0;x_2) \\ R(x_1;x_0) & R(x_1;x_1) & R(x_1;x_2) \\ R(x_2;x_0) & R(x_2;x_1) & R(x_2;x_2) \\ \end{bmatrix} \times \begin{bmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \end{bmatrix}
소거법(cancelation)을 이용하면 α⃗=R−1×x⃗\vec{\alpha}=R^{-1}\times \vec{x}가 되고 이를 통해 α\alpha를 구하면 된다. 커널함수는 보통 가우시안 함수 e−r22σe^{\frac{-r^2}{2\sigma}}를 사용하고 TPS는 r2log⁡(r)r^2\log(r)를 활용한다.
RBF를 사용한 보간법은 많은 과정에서 활용가능하지만, 이미지와 같이 2차원 이상의 데이터에서 국소적인 변화를 다루어야 하는 경우에는 한계가 있다. 이런 문제를 해결하기 위해 제안된 방법이 바로 TPS(Thin Plate Spline)이다. TPS는 2차원 이상의 데이터에서도 스무스한 보간을 가능하게 하며, 동시에 국소적인 변화를 효과적으로 다룰 수 있다. 따라서 이미지와 같은 고차원 데이터에서의 와핑문제에 매우 적합하다.

Thin Plate Spline(TPS)

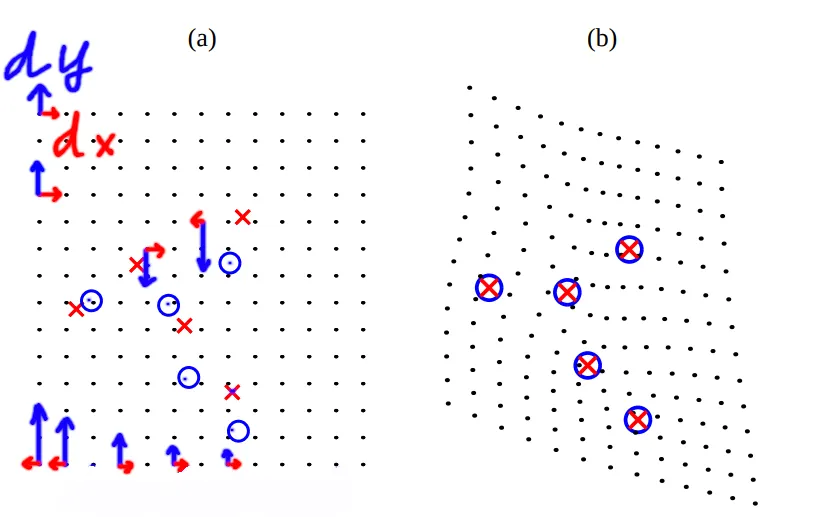
지금 부턴 본격적으로 TPS에 대해 설명한다. 아래 그림과 같이 2차원 이미지에서 붉은색 X표시의 점을 파란색 O표시의 점으로 옮기는 상황을 다룬다.
image is from Khanh’s blog
2차원이므로 아래와 같이 두개의 스무스함수가 필요하다.
fx′(x,y)=a1+axx+ayy+∑i=1NwiU(∣∣(xi,yi)−(x,y)∣∣)f_{x'}(x,y)=a_1+a_{x}x+a_{y}y+\sum^{N}_{i=1}w_iU(||(x_i,y_i)-(x,y)||)
fy′(x,y)=a1+axx+ayy+∑i=1NwiU(∣∣(xi,yi)−(x,y)∣∣)f_{y'}(x,y)=a_1+a_{x}x+a_{y}y+\sum^{N}_{i=1}w_iU(||(x_i,y_i)-(x,y)||)
두 함수는 컨트롤포인트 (xi,yi)(x_i,y_i)를 (xi′,yi′)(x_i',y_i')로 옮긴다. 수식에서 a1+a2x+a3ya_1+a_2x+a_3y는 선형변환을 표현하고 ∑i=1NwiU(∣∣(xi,yi)−(x,y)∣∣)\sum^{N}_{i=1}w_iU(||(x_i,y_i)-(x,y)||)는 커널함수를 통한 변환을 의미한다.
U(∣∣((xi−yi)−(x,y))∣∣)U(||((x_i-y_i)-(x,y))||)는 (xi,yi)(x_i,y_i)를 중심으로 하는 커널함수로 함수 U(.)U(.)UUU(r)=r2log⁡(r)U(r)=r^2\log(r)로 정의되고 그림으로 그리면 아래와 같다.
image is from Khanh’s blog
그림에서 보이는것 처럼 중심에서 멀어질수록 작아지는 함수라 볼 수 있다. 이 커널을 각 컨트롤포인트마다 가중치를 넣어 적용하게 되면 아래와 같은 그림으로 표현될 수 있다.
image is from Khanh’s blog
식으로 돌아와서, 우리가 구해야 하는 값은 각 스플라인함수의 계수 (a,ax,ay,wi)(a,a_x,a_y,w_i)로 아래식을 풀어야 한다.
L=[KPPTO]×[wa]=[vo]L= \begin{bmatrix} K & P \\ P^T & O \end{bmatrix} \times \begin{bmatrix} w \\ a \end{bmatrix} = \begin{bmatrix} v \\ o \end{bmatrix}
여기서 Kij=U(∣∣((xi−yi)−(xj,yj))∣∣)K_{ij}=U(||((x_i-y_i)-(x_j,y_j))||)이고 PP는 (1,xi,yi)(1,x_i,y_i)이다. 위쪽에 해당하는 [KP]×[wa]T\begin{bmatrix} K & P \end{bmatrix} \times \begin{bmatrix} w & a \end{bmatrix}^T는 위에서 언급한 스무스함수를 통해 변환된 컨트롤포인트를 의미한다. 아래쪽에 해당하는 [PTO]×[wa]T\begin{bmatrix} P^T & O \end{bmatrix} \times \begin{bmatrix} w & a \end{bmatrix}^T는 제한조건이며 아래 수식을 의미한다. 해당 수식의 의미는 본 페이지에선 추가로 설명하지 않는다.
∑i=1Nwi=0∑i=1Nwixi=∑i=1Nwiyi=0\begin{matrix} \sum^N_{i=1}w_i=0 \\ \sum^N_{i=1}w_i x_i = \sum^N_{i=1}w_i y_i = 0 \end{matrix}
예를 들어 정리하면 만약 세개의 컨트롤포인트 (x0,y0),(x1,y1),(x2,y2)(x_0,y_0),(x_1,y_1),(x_2,y_2)가 있다고 할 때 TPS함수 fx′f_{x'}는 아래와 같이 정리된다.
[K00K10K201x0y0K01K11K211x1y1K02K12K221x2y2111000x0x1x2000y0y1y2000]×[w0w1w2a0axay]=[x0′x1′x2′000]\begin{bmatrix} K_{00} & K_{10} & K_{20} & 1 & x_0 & y_0 \\ K_{01} & K_{11} & K_{21} & 1 & x_1 & y_1 \\ K_{02} & K_{12} & K_{22} & 1 & x_2 & y_2 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ x_0 & x_1 & x_2 & 0 & 0 & 0 \\ y_0 & y_1 & y_2 & 0 & 0 & 0 \\ \end{bmatrix} \times \begin{bmatrix} w_0 \\ w_1 \\ w_2 \\ a_0 \\ a_x \\ a_y \end{bmatrix} = \begin{bmatrix} x_0' \\ x_1' \\ x_2' \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}
같은 방법으로 fy′f_y'은 아래와 같다.
[K00K10K201x0y0K01K11K211x1y1K02K12K221x2y2111000x0x1x2000y0y1y2000]×[w0w1w2a0axay]=[y0′y1′y2′000]\begin{bmatrix} K_{00} & K_{10} & K_{20} & 1 & x_0 & y_0 \\ K_{01} & K_{11} & K_{21} & 1 & x_1 & y_1 \\ K_{02} & K_{12} & K_{22} & 1 & x_2 & y_2 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ x_0 & x_1 & x_2 & 0 & 0 & 0 \\ y_0 & y_1 & y_2 & 0 & 0 & 0 \\ \end{bmatrix} \times \begin{bmatrix} w_0 \\ w_1 \\ w_2 \\ a_0 \\ a_x \\ a_y \end{bmatrix} = \begin{bmatrix} y_0' \\ y_1' \\ y_2' \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}

참고링크