//
Search
📏

Norm

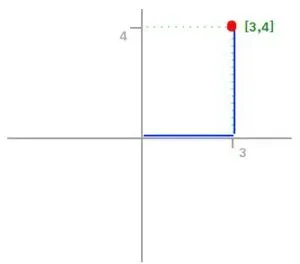
Norm은 벡터의 전체길이 혹은 크기를 측정하는 방법이다. Norm으로 측정한 벡터의 크기는 Magnitude라 한다. 본 문서에선 L0L^0, L1L^1, L2L^2, L∞L^{\infty}을 소개한다.

사전지식

V⊆F⊂CV \sube F \sub \mathbb{C}이라 하고 함수 f:V→Rf:V\rightarrow\mathbb{R}가 아래 세 조건을 만족할 때,
a∈F,    u,v∈Va \in F, \;\;u,v\in V에 대하여 1. f(au)=∣a∣⋅f(u)f(a\mathbf{u}) = |a|\cdot f(\mathbf{u}) 2. f(u+v)≤f(u)+f(v)f(\mathbf{u+v}) \le f(\mathbf{u}) + f(\mathbf{v}) (→\rightarrow삼각 부등식) 3. 만약 f(u)=0f(\mathbf{u})=0이면 u\mathbf{u}는 영벡터이다.
함수 ff를 노름(Norm)이라 한다. 세가지 성질 중 1,2번 만족하는 경우는 반노름(seminorm)이라 한다. 노름은 그 값이 항상 0보다 크거나 같으며 이는 1,2번 조건으로 부터 유도되기 때문에 반노름의 성질이기도 하다. (f(u)≥0f(\mathbf{u}) \ge0)

L0L^0(L0  normL_0\;norm)

L0  normL_0\;norm 함수 ff의 정의는 아래와 같다.
f:∣x1∣0+∣x2∣0+⋯+∣xn∣0.∣xk∣0={1xk∈R\{0}0xk=0,  k∈Nf:|x_1|^0+|x_2|^0+\cdots+|x_n|^0. \\ |x_k|^0= \begin{cases} 1 & x_k\in \mathbb{R}\backslash\{0\}\\ 0 & x_k=0 \end{cases} ,\; k\in\mathbb{N}
위 수식은 결국 0이 아닌 원소의 개수를 의미한다. 예를 들어 a=(1,0)a=(1,0)에 대해 f(a)f(a)은 0이 아닌 원소의 개수가 1개다. 따라서 f(a)=1f(a)=1이다.
L0−NormL_0-Norm은 사실 위 노름의 조건 중 1번 조건을 만족하지 않으므로 노름이 아니다.

L1L^1(L1  normL_1\;norm)

L1  normL_1\;norm은 맨하탄 거리(Manhattan Distance) 또는 택시노름(Taxicab norm)이라고도 한다. L0−NormL_0-Norm은 공간상의 벡터의 크기를 의미한다. 이를 측정하는 가장 쉬운 방법은 벡터 거리의 절대값의 합을 구하는 것이다.
f:∣∣x∣∣1=∣x1∣+∣x2∣+⋯+∣xn∣=∑k=1n∣xk∣f:||x||_1=|x_1|+|x_2|+\cdots+|x_n|=\sum^n_{k=1}{|x_k|}
a=(3,4)a=(3,4)에 대해 f(a)=∣3∣+∣4∣=7f(a)=|3|+|4|=7이 된다. 머신러닝이나 통계학에선 L1L_1정규화 개념으로 많이 등장한다.

L2L^{2}(L2  normL_2\;norm)

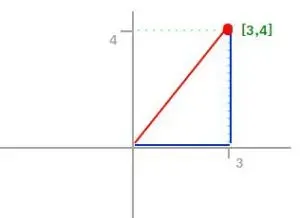
가장 많이 사용되는 노름으로 유클리디안 노름(Euclidean norm)이라고도 한다.
∣∣x∣∣2=x12+x22+⋯+xn2=∑k=1nxk2||x||_2=\sqrt{x_1^2+x_2^2+\cdots+x_n^2} = \sqrt{\sum^n_{k=1}{x_k^2}}
a=(3,4)a=(3,4)에 대해 f(a,b)=32+42=9+16=5f(a,b)=\sqrt{3^2+4^2}=\sqrt{9+16}=5이 된다.

L∞L^{\infty}(L−infinity  normL-infinity\;norm)

∣∣x∣∣∞=max⁡(∣x1∣,∣x2∣,⋯ ,∣xn∣)||x||_{\infty} = \max(|x_1| , |x_2|, \cdots, |x_n|)
벡터의 원소에서 최대크기를 구하는 함수다. a=(3,4)a=(3,4)에 대해 가장 큰 원소는 44이므로 f(a)=4f(a)=4가 된다.

참고문헌