///
Search
📄

Chapter 3

Approximation in the L2L^2-norm

체비셰프는 uniform−normuniform-norm에 대한 근사문제를 풀고싶어했다. 본 챕터에서는 uniform−normuniform-norm을 다루기 전에 L2−normL^2-norm에서 먼저 근사문제를 풀어본다. 이후 챕터에서 uniform−normuniform-norm에 대해 다뤄볼것이다.

3.1 Best approximation in the L2L^2-norm

연속함수 f(x)∈C[a,b]f(x)\in C[a,b]라 정의하자. 이 때 L2−normL^2-norm에서 f(x)f(x)에 최적 근사한(the best approximating) nn차 다항식 p(x)∈Pnp(x)\in \mathcal{P}_n를 찾고자 한다. 이를 위해 아래 과정을 진행하였다.

Problem 1

f(x)∈C[a,b]f(x)\in C[a,b]과 아래 식과 같은 L2L^2-norm에 대해 가장 근사한 nn차 다항식 p∈Pnp \in \mathcal{P}_n을 찾아라
∣∣f−p∣∣2=inf⁡q∈Pn∣∣f−q∣∣2.||f-p||_2=\inf_{q\in \mathcal{P}_n}{||f-q||_2}.
이 때 가장 근사한 다항식 p(x)p(x)는 항상 유일하게 존재하며 이에 대한 증명은 본 교재에선 생략하였다. 대신 이후 uniform-norm에 대해선 이후 챕터4에서 증명과정을 다룰것이다.
해당 문제를 풀기 위해 최소화 해야하는 값은 아래와 같다.
E=∣∣f−p∣∣2=(∫ab∣f(x)−p(x)∣2)12,∣∣f∣∣22=∫abf(x)2dx.E=||f-p||_2=(\int_{a}^{b}{|f(x)-p(x)|}^2)^{\frac{1}{2}}, \\ ||f||^2_2=\int^{b}_{a}{f(x)}^2 dx.

Theorem 1

아래식을 만족하는 최적 근사 다항식 p∈Pnp \in \mathcal{P}_n
∣∣f−p∣∣2=min⁡q∈Pn∣∣f−q∣∣2.||f-p||_2=\min_{q\in \mathcal{P}_n}{||f-q||_2}.
의 필요충분 조건(iff\mathbf{iff})은
⟨f−p,q⟩=0, ∀q∈Pn\langle f-p, q \rangle=0,\space \forall q \in \mathcal{P}_n
이고 아래 조건을 만족한다.
⟨f,q⟩=∫abf(x)g(x)dx.\langle f,q \rangle=\int_{a}^{b}{f(x)g(x)}dx.
⟨f,q⟩=∫abf(x)g(x)dx\langle f,q \rangle=\int_{a}^{b}{f(x)g(x)}dx은 다항식에서 내적의 정의를 의미한다.
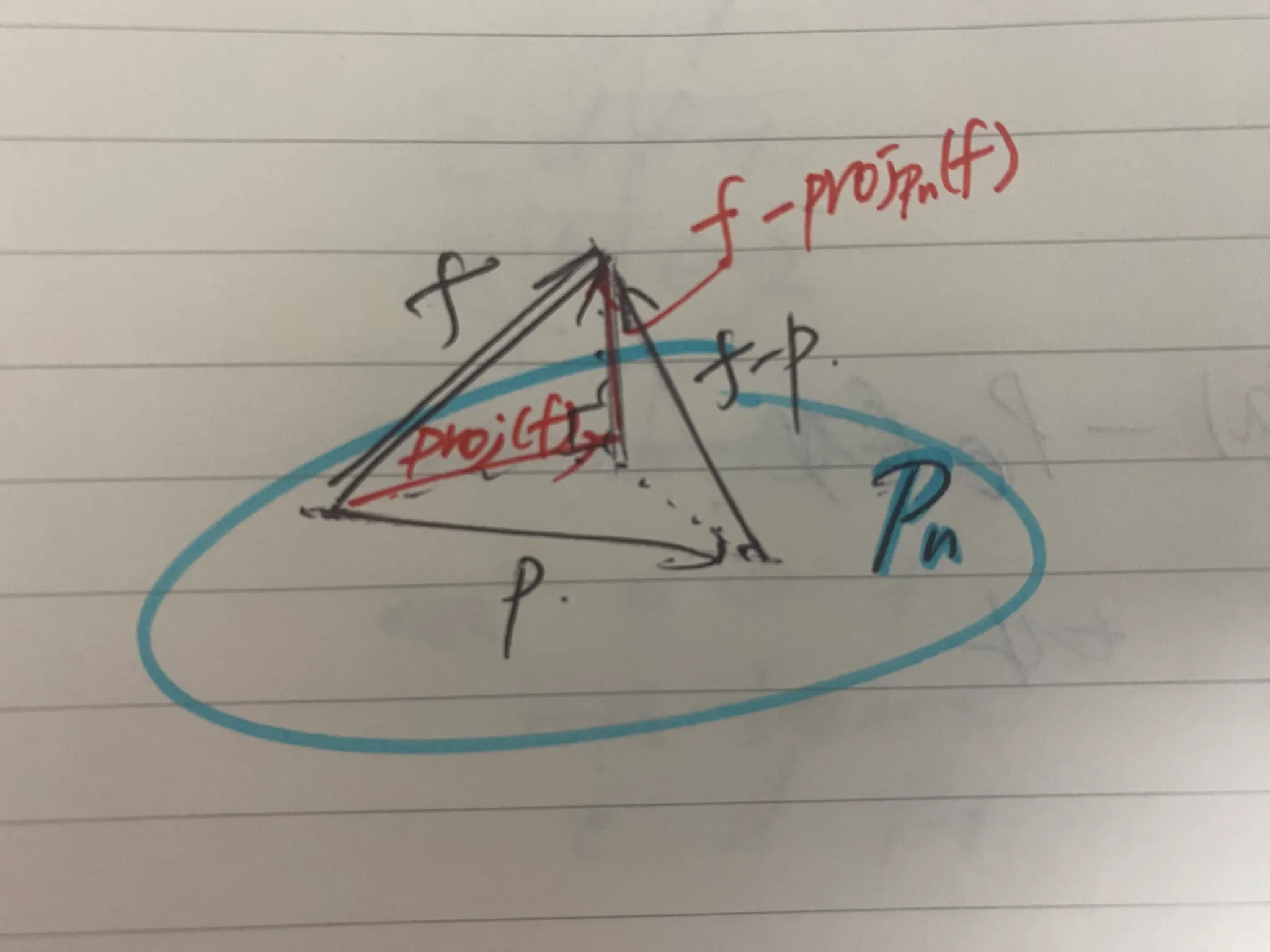
위의 그림을 참고하면 삼각부등식에 의해 부분공간 Pn\mathcal{P}_n에서 어떤 값을 가져와도 함수 f(x)f(x)의 정사영값 projPn(f)proj_{\mathcal{P}_n}{(f)}보다 작을 수 없다. 즉, 적분값은 p(x)p(x)가 부분공간 Pn\mathcal{P}_n에서 함수 f(x)f(x)의 정사영(orthogonal projection) 일 때 최소화된다. 이는 위 수식 ⟨f−p,q⟩=0, ∀q∈Pn\langle f-p, q \rangle=0,\space \forall q \in \mathcal{P}_n이 성립하는 이유를 설명한다.
정리하면 PnP_n의 직교기저(orthogonal basis)를 u1,u2,u3,...,unu_1,u_2,u_3,...,u_n라 하면 아래 식을 만족한다.
p(x)=⟨f,u1⟩⟨u1,u1⟩u1(x)+⟨f,u2⟩⟨u2,u2⟩u2(x)+⋯+⟨f,un⟩⟨un,un⟩un(x)p(x)=\frac{\langle f, u_1 \rangle}{\langle u_1, u_1 \rangle}{u_1(x)}+ \frac{\langle f, u_2 \rangle}{\langle u_2, u_2 \rangle}{u_2(x)}+ \cdots+ \frac{\langle f, u_n \rangle}{\langle u_n, u_n \rangle}{u_n(x)}
직교 다항식(orthogonal polynomials)은 내적공간 VV의 기저(basis)에 그램-슈미트 과정(Gram-Schmidt Process)을 적용하여 구할 수 있다.

3.1.1 The Gram-Schmidt Process

{x1,x2,⋯ ,xn}\{x_1,x_2,\cdots,x_n\}를 내적공간 VV의 기저(basis)라고 하면 아래 수식을 만족한다.
u1=(1∣∣x1∣∣)x1uk+1=1∣∣xk+1−pk∣∣(xk+1−pk) for k=1,⋯ ,n−1.pk=⟨xk+1,u1⟩u1+⟨xk+1,u2⟩u2+⋯+⟨xk+1,uk⟩.\begin{align*}&u_1=\Bigg(\frac{1}{||x_1||} \Bigg)x_1 \\ &u_{k+1}=\frac{1}{||x_{k+1}-p_k||}(x_{k+1}-p_k) \space for \space k=1,\cdots,n-1. \\ &p_k=\langle x_{k+1}, u_1 \rangle u_1 + \langle x_{k+1}, u_2 \rangle u_2 + \cdots + \langle x_{k+1}, u_k \rangle. \end{align*}
pkp_k는 span(u1,u2,⋯ ,unu_1, u_2, \cdots, u_n)에 xk+1x_{k+1}를 사영(projection)한 값이며 {u1,u2,⋯ ,un}\{ u_1, u_2, \cdots, u_n \}은 공간 VV의 정규 직교 벡터다.

3.1.2 Example

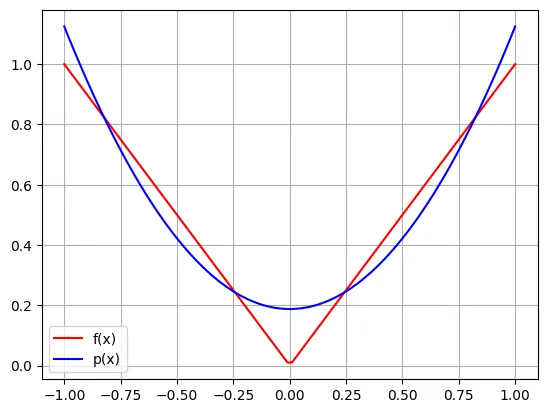
범위 [−1,1][-1,1]에서 f(x)=∣x∣f(x)=|x| 에 최적근사한 이차다항식을 찾으시오.
이를 해결하기 위해 아래 식을 최소화 시켜야한다.
∣∣f−p∣∣2=(∫ab∣f(x)−p(x)∣2dx)12=∣∣∣x∣−p∣∣2=(∫−11∣∣x∣−p(x)∣2dx)12.||f-p||_2=\Bigg(\int_a^b|f(x)-p(x)|^2dx\Bigg)^{\frac{1}{2}}=|||x|-p||_2=\Bigg(\int_{-1}^{1}{||x|-p(x)|^2dx\Bigg)^{\frac{1}{2}}}.
L2−normL^2-norm에서 최소화 하기 위해선 p(x)p(x)가 2차 다항식의 부분공간에서 f(x)f(x)의 정사영이 되야한다.
내적공간 VV에 대한 2차다항식의 기저는 {1,x,x2}\{1,x,x^2\}로 잡을 수 있다.
u1=(1∣∣x1∣∣)x1=12p1=⟨x2,u1⟩u1=⟨x,12⟩12=0u2=1∣∣x2−p2∣∣(x2−p1)=1∣∣x∣∣x=32xp2=⟨x3,u1⟩u1+⟨x3,u2⟩u2=⟨x2,12⟩12+⟨x2,32x⟩32x=13u3=1∣∣x3−p2∣∣(x3−p2)=1∣∣x2−13∣∣(x2−13)=458(x2−13).\begin{align*}&u_1 =&\Bigg(\frac{1}{||x_1||} \Bigg)x_1 &=\frac{1}{\sqrt{2}} \\ &p_1 =&\langle x_2,u_1 \rangle u_1=\langle x, \frac{1}{\sqrt{2}}\rangle \frac{1}{\sqrt{2}} &= 0 \\ &u_2=&\frac{1}{||x_2-p_2||}(x_2-p_1)=\frac{1}{||x||}x &= \frac{\sqrt{3}}{\sqrt{2}}x \\ &p_2=&\langle x_3,u_1 \rangle u_1 + \langle x_3, u_2 \rangle u_2 = \langle x^2, \frac{1}{\sqrt{2}} \rangle\frac{1}{\sqrt{2}} + \langle x^2, \frac{\sqrt{3}}{\sqrt{2}} x \rangle\frac{\sqrt{3}}{\sqrt{2}}x &=\frac{1}{3} \\ &u_3=&\frac{1}{||x_3-p_2||}(x_3-p_2)=\frac{1}{||x^2-\frac{1}{3}||}(x^2-\frac{1}{3}) &=\frac{\sqrt{45}}{\sqrt{8}}(x^2-\frac{1}{3}). \end{align*}
이 때, 위 Theorem 1에 의해서 아래 식을 계산할 수 있다.
p(x)=⟨f,u1⟩⟨u1,u1⟩u1(x)+⟨f,u2⟩⟨u2,u2⟩u2(x)+⟨f,u3⟩⟨u3,u3⟩u3(x).p(x)=\frac{\langle f, u_1 \rangle}{\langle u_1, u_1 \rangle}u_1(x) +\frac{\langle f, u_2 \rangle}{\langle u_2, u_2 \rangle}u_2(x) + \frac{\langle f, u_3 \rangle}{\langle u_3, u_3 \rangle}u_3(x).
⟨u1,u1⟩=∫−1112dx=1⟨f,u1⟩=12∫−11∣x∣dx=22∫01xdx=12⟨u2,u2⟩=32∫−11x2dx=1⟨f,u2⟩=32∫−11∣x∣xdx=0⟨u3,u3⟩=∫−11(458(x2−13))2dx=1⟨f,u3⟩=458∫−11∣x∣(x2−13)dx=542.\begin{align*} \langle u_1, u_1 \rangle =& \int^{1}_{-1}{\frac{1}{2}}dx &=1 \\ \langle f, u_1 \rangle =& \frac{1}{\sqrt{2}}\int^{1}_{-1}|x|dx = \frac{2}{\sqrt{2}}\int^{1}_{0}xdx &= \frac{1}{\sqrt{2}} \\ \langle u_2, u_2 \rangle =& \frac{3}{2}\int^{1}_{-1}{x^2}dx &=1 \\ \langle f, u_2 \rangle =& \frac{\sqrt{3}}{\sqrt{2}}\int^{1}_{-1}{|x|}xdx &=0 \\ \langle u_3, u_3 \rangle =& \int^{1}_{-1}({\frac{\sqrt{45}}{8}}(x^2-\frac{1}{3}))^2dx &=1 \\ \langle f, u_3 \rangle =& {\frac{\sqrt{45}}{8}}\int^{1}_{-1}{|x|(x^2-\frac{1}{3})}dx &=\frac{\sqrt{5}}{4\sqrt{2}}. \end{align*}
따라서 아래와 같이 p(x)p(x)가 구해지며 그래프를 통해 시각화 할 수 있다.
p(x)=12+1516x2−516=1516x2+316,p(x)=\frac{1}{2} + \frac{15}{16}x^2-\frac{5}{16} = \frac{15}{16}x^2 + \frac{3}{16},
import numpy as np import matplotlib.pyplot as plt # 함수 정의 def f(x): return abs(x) def p(x): return 15/16*(x**2) + 3/16 # 값 정의 x = np.linspace(-1, 1, 100) fy = f(x) py = p(x) # 시각화 ax = plt.axes() ax.plot(x,fy, 'r', label='f(x)') ax.plot(x, py, 'b', label='p(x)') plt.legend(loc='best', ncol=1) plt.grid()
Python
복사
가 되고 최대오차는
E=(∫−11∣∣x∣−1516x2−316∣2dx)12=196≈0.1021.E=\Bigg( \int^{1}_{-1} \bigg| |x| - \frac{15}{16}x^2 - \frac{3}{16} \bigg|^2 dx \Bigg)^{\frac{1}{2}} = \frac{1}{\sqrt{96}} \approx0.1021.

3.1.3 Legendre polynomials

아래 식과 같은 직교함수를 가지는 다항식을 르장드르 다항식(Legendre polynomials)이라고 한다.
⟨f,q⟩=∫−11f(x)g(x)dx\langle f,q \rangle=\int_{-1}^{1}{f(x)g(x)}dx
즉, 범위 [a,b][a, b]가 [−1,1][-1,1]인 경우로 아래식과 같이 전개할 수 있다.
p(x)=⟨f,P0⟩⟨P0,P0⟩P0(x)+⟨f,P1⟩⟨P1,P1⟩P1(x)+⋯+⟨f,Pn−1⟩⟨Pn−1,Pn−1⟩Pn−1(x).p(x)=\frac{\langle f, P_0 \rangle}{\langle P_0, P_0 \rangle}P_0(x) +\frac{\langle f, P_1 \rangle}{\langle P_1, P_1 \rangle}P_1(x) + \cdots + \frac{\langle f, P_{n-1} \rangle}{\langle P_{n-1}, P_{n-1} \rangle}P_{n-1}(x).
또한 르장드르 다항식은 아래 관계식도 성립한다.
(n+1)Pn+1(x)=(2n+1)xPn(x)−nPn−1(x).(n+1)P_{n+1}(x) = (2n + 1)xP_n(x) - nP_{n-1}(x).
결국 이러한 조건을 가진 다항식을 근사할 땐 일정한 값이 존재하므로 사전에 계산된 값들을 이용하여 위 그램-슈미트 과정 등의 계산이 필요없이 값을 바로 대입하여 활용할 수 있다. 값은 표로 정리되어 본 교재의 뒤 쪽에 적혀있다.