///
Search
📄

Chapter 4

Approximation in the uniform norm

파프누티 리보비치 체비셰프는 uniform-norm에서 최적함수를 구하기 위한 아이디어를 처음 낸 사람이다. 그는 스스로 아래 문제를 제시하고 이에 대한 해법을 제시하기 위한 과정을 진행하였다. Problem 2. 폐구간 [a,b][a,b]에서 정의된 연속함수 f(x)f(x)에 대해 임의의 점 x∈[a,b]x \in [a,b]에서 maximum errormaximum\space error 기준으로 f(x)f(x)를 nn차 다항식 p(x)=∑k=0nakxkp(x)=\sum^{n}_{k=0}{a_kx^k}로 표현할 수 있는가? (여기서 n∈Zn \in \mathbb{Z}) 즉, 에러 max⁡a≤x≤b∣f(x)−p(x)∣\max_{a\le x \le b}{|f(x)-p(x)|}를 최소화하는 p(x)p(x)를 구할 수 있는가를 문제로 정의하였다. 본 챕터는 이 문제에 대해 다루는 챕터이다. 여기선 이러한 함수가 있는지(exists, 존재성)와 유일한가(unique, 유일성)에 대해 다뤄볼것이다.

4.1 Existence

1854년에 체비셰프는 최적근사문제에 대한 솔루션을 찾았다.

Lemma 1.

f(x)∈C[a,b]f(x) \in C[a,b]에 대해 부분공간 Pn\mathcal{P}_n에서 최적근사하는 함수를 p(x)p(x)라 하자(여기서 CC는 연속함수(continuous function)을 의미한다). 이 때, f(x1)−p(x1)=−(f(x2)−p(x2))=∣∣f(x)−p(x)∣∣∞f(x_1)-p(x_1)=-(f(x_2)-p(x_2))=||f(x)-p(x)||_{\infty}를 만족하는 서로 다른 점 x1,x2∈[a,b]x_1,x_2 \in [a,b]가 최소 두 개 존재한다.
Proof. 귀류법(contradiction)을 이용하여 증명한다. 귀류법은 어떤 명제가 ‘참’임을 주장하려 할 때, 이를 거꾸로 ‘거짓’이라고 가정하고 이 때 모순을 지적하여 최종적으로 해당 명제가 ‘참’ 임을 보이는 방법이다.
먼저 손실값을 정의하면 E=∣∣f−p∣∣∞=max⁡a≤x≤b∣f−p∣E=||f-p||_{\infty}=\max_{a\le x \le b}{|f-p|}가 된다. 만약에 위 lemma가 거짓이라면 위 식을 만족하는 점은 한 개만 존재한다고 할 수 있다. 따라서 f(x1)−p(x1)=Ef(x_1)-p(x_1)=E가 성립하는 어떤 x1x_1가 존재한다. 여기서 최소손실값 ϵ\epsilon에 대해선 아래 식이 성립한다.
ϵ=min⁡a≤x≤b(f(x)−p(x))>−E, ∀x∈[a,b]\epsilon = \min_{a \le x \le b}{(f(x)-p(x)) > -E}, \space \forall x \in [a,b]
위 식은 최대손실값이 EE이므로 최소손실값은 최대손실값에 마이너스를 곱한 −E-E보다 작을 순 없기 때문에 성립한다. 때문에 E+ϵ≠0E+\epsilon \ne 0이고 따라서 q=p+E+ϵ2∈Pn, p≠qq = p + \frac{E+\epsilon}{2} \in \mathcal{P}_n, \space p \ne q를 만족하는 qq에 대해 정의할 수 있다. 이에 따라 식을 전개하면
ϵ≤f(x)−p(x)≤Eϵ−E+ϵ2≤f(x)−p(x)−E+ϵ2≤E−E+ϵ2ϵ−E+ϵ2≤f(x)−q(x)≤E−E+ϵ2−E−ϵ2≤f(x)−q(x)≤E−ϵ2, ∀x∈[a,b]\begin{align*} \epsilon &\le f(x)-p(x) \le E \\ \epsilon - \frac{E+\epsilon}{2} &\le f(x)-p(x) - \frac{E+\epsilon}{2} \le E - \frac{E+\epsilon}{2} \\ \epsilon - \frac{E+\epsilon}{2} &\le f(x)- q(x) \le E - \frac{E+\epsilon}{2} \\ - \frac{E-\epsilon}{2} &\le f(x)- q(x) \le \frac{E-\epsilon}{2}, \space \forall x \in [a,b] \end{align*}
가 되고 정리하면
∣∣f−q∣∣∞≤E−ϵ2≤E=∣∣f−p∣∣∞||f-q||_{\infty} \le \frac{E-\epsilon}{2} \le E = ||f-p||_{\infty}
가 된다. 이는 ∣∣f−q∣∣∞||f-q||_{\infty}의 값이 ∣∣f−p∣∣∞||f-p||_{\infty}보다 작다는 것이며 이는 함수 ff의 최적근사함수는 qq라는 가정에 위배되므로 모순이다. 이에 따라 귀류법에 의해 lemma 1은 참이다.

Corollary 1.

f(x)∈C[a,b]f(x) \in C[a,b]에서 최적근사함수의 상수값은
p0=12[max⁡a≤x≤bf(x)+min⁡a≤x≤bf(x)]p_0 = \frac{1}{2} \Bigg[ \max_{a \le x \le b}{f(x)} + \min_{a \le x \le b}{f(x)} \Bigg]
이고 손실값은
E0(f)=12[max⁡a≤x≤bf(x)−min⁡a≤x≤bf(x)]E_0(f) = \frac{1}{2} \Bigg[ \max_{a \le x \le b}{f(x)} - \min_{a \le x \le b}{f(x)} \Bigg]
를 만족한다.
Proof. 다시 귀류법을 통해 증명한다. 먼저 f(x1)−p0=−(f(x2)−p0)=∣∣f−p0∣∣∞f(x_1)-p_0 = -(f(x_2)-p_0) = ||f-p_0||_{\infty}를 만족하는 x1,x2x_1, x_2를 잡는다. 만약 p0=12[max⁡a≤x≤bf(x)+min⁡a≤x≤bf(x)]p_0 = \frac{1}{2} \bigg[ \max_{a \le x \le b}{f(x)} + \min_{a \le x \le b}{f(x)} \bigg]가 아닌 다른값 dd라고 가정하면
E(x1)=f(x1)−dE(x2)=f(x2)−d\begin{align*} E(x_1) &= f(x_1)-d \\ E(x_2) &= f(x_2)-d \end{align*}
이고 이는 E(x1)+E(x2)≠0E(x_1)+E(x_2) \ne0을 보인다. 이는 lemma 1과 모순된다.
다음으로 lemma 1을 일반화하여 최적 선영근사가 있을경우 최적 근사 다항식의 차수를 나타내는 nn에 대해 f−pf-p가 ±∣∣f−p∣∣∞\pm || f-p ||_{\infty}사이에 부호가 번갈아 나타나는 점이 적어도 n+2n+2개 존재함을 보이고자 한다.
이 일반화를 보이기 위해 먼저 몇가지 정의를 해야한다.

Definition 1.

연속함수 f(x)∈C[a,b]f(x) \in C[a, b]에서 만약 f(x)f(x)에 대해 f(x)=∣∣f∣∣∞f(x)=||f||_{\infty}면 x∈[a,b]x \in [a,b]는 (+)point라 한다. 만약 f(x)f(x)에 대해 f(x)=−∣∣f∣∣∞f(x)=-||f||_{\infty}면 x∈[a,b]x \in [a,b]는 (-)point라 한다. 만약 f(x)f(x)에 대해 xix_i가 (+)point와 (-)point로 반복되는 값이면 서로 다른점들 a≤x0<x1<⋯<xn≤ba \le x_0 < x_1 < \cdots < x_n \le b의 집합을 alternating set이라 한다. 이는 모든 ii에 대해 ∣f(xi)∣=∣∣f∣∣∞|f(x_i)|=||f||_{\infty}고 f(xi)=−f(xi−1)f(x_i)=-f(x_{i-1})를 만족한다는 것을 말한다.
위 개념을 활용하여 lemma 1을 일반화시키고 최적 근사 다항식에 대한 특징을 보이려 한다.

Theorem 2.

f(x)∈C[a,b]f(x) \in C[a,b]에 대해 p(x)p(x)가 Pn\mathcal{P}_n에서 최적근사함수라 하자. 이때, f−pf-p의 alternating set이 최소 n+2n+2개 존재한다.
Proof. f(x)∈Pnf(x) \in \mathcal{P}_n이면 f(x)=p(x)f(x)=p(x)이므로 이 경우엔 f−p=0f-p=0이므로 f−pf-p의 alternating set이 존재하지 않는다. 따라서 f(x)∉p(x)f(x) \notin p(x)이다.
(균등)연속함수 ϕ=f−p\phi=f-p를 잡는다(Compact set에서 연속하면 균등연속이다). 다음 단계는 폐구간 [a,b][a,b]에서 작은구간값을 가지도록 a=t0<t1<⋯<tk=ba=t_0<t_1<\cdots<t_k=b를 x,y∈[ti;tt+1]x,y\in[t_i;t_{t+1}]면 ∣ϕ(x)−ϕ(y)∣<E2|\phi(x)-\phi(y)|<\frac{E}{2}를 만족하도록 잡는다. 즉 모든 구간에서 값이 E2\frac{E}{2}를 넘지 않도록 한다.
만약 폐구간 [ti;tt+1][t_i;t_{t+1}]에서 ϕ=f−p\phi=f-p에 대해 (+)point를 포함하면 ϕ\phi는 폐구간 [ti;tt+1][t_i;t_{t+1}]에서 전부 양수이다.
x,y∈[ti,tt+1]          and          ϕ(x)=E          ⇒          ϕ(y)>E2.                    (4.1)x,y\in[t_i,t_{t+1}] \;\;\;\;\; and \;\;\;\;\; \phi(x)=E\;\;\;\;\;\Rightarrow\;\;\;\;\;\phi(y) > \frac{E}{2}.\;\;\;\;\;\;\;\;\;\; (4.1)
유사하게 만약 폐구간 [ti;tt+1][t_i;t_{t+1}]에서 ϕ=f−p\phi=f-p에 대해 (-)point를 포함하면 ϕ\phi는 폐구간 [ti;tt+1][t_i;t_{t+1}]에서 전부 음수이다. 따라서 어떤 구간도 (+)point와 (-)point를 모두 포함할 순 없다. 때문에 (+)point를 포함하는 구간을 (+)interval이라 부를 수 있고 (-)point를 포함하는 구간을 (-)interval이라 부를 수 있다. 따라서 interval은 0을 포함하는 interval에 의해 나눠질 수 있게 된다.
다음 단계로 각 interval을 라벨링 한다. 여기서 II의 인덱스는 전체 구간을 순서대로 인덱싱한것이 아니라 interval에 대한 인덱싱이다.
I1,I2,⋯ ,Ik1                                        (+)intervalsIk1+1,Ik1+2,⋯ ,Ik2                                        (−)intervals⋯⋯⋯⋯⋯⋯⋯                                        ⋯⋯⋯⋯⋯Ikm−1+1,Ikm+2,⋯ ,Ikm                                        (−1)m−1intervals\begin{align*} I_1,I_2,\cdots, I_{k_1} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\mathbf{(+)intervals} \\ I_{k_1+1},I_{k_1+2},\cdots,I_{k_2} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\mathbf{(-)intervals}\\ \cdots\cdots\cdots\cdots\cdots\cdots\cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\cdots\cdots\cdots\cdots\cdots \\ I_{k_{m-1}+1},I_{k_m+2},\cdots,I_{k_m} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&(-1)_{m-1}\mathbf{intervals} \end{align*}
SS를 모든 부호가 있는 intervals((++)interval, (−-)interval)의 합집합이라고 하자. S=⋃j=1kmIj.S=\bigcup_{j=1}^{km}{I_j}. 그리고 NN은 나머지 intervals(0을 포함하는 intervals)의 합집합이라고 하자. SS와 NN은 S∪N=[a,b]S\cup N=[a,b]에서 compact set이다.
우리가 증명하고 싶은것은 interval의 개수 mm이 m≥n+2m\ge n+2를 만족하는 것이며 이를 귀납법으로 증명하기 위해 m<n+2m<n+2라 가정하자.
(++)interval과 (−-)interval는 서로 separated하므로 점 z1,⋯ ,zm−1∈Nz_1,\cdots,z_{m-1} \in N 을 아래와 같이 표현할 수 있다.
max⁡Ik1<        z1<min⁡Ik1+1      max⁡Ik2<        z2<min⁡Ik2+1      ⋯⋯⋯⋯⋯⋯                max⁡Ikm−1<    zm−1<min⁡Ikm−1+1\begin{align*} \max{I_{k_1}} &< \;\;\;\;z_1 &< \min{I_{k_1+1}}\;\;\; \\ \max{I_{k_2}} &< \;\;\;\;z_2 &< \min{I_{k_2+1}}\;\;\; \\ \cdots\cdots\cdots& &\cdots\cdots\cdots\;\;\;\;\;\;\;\;\\ \max{I_{k_{m-1}}} &< \;\;z_{m-1} &< \min{I_{k_{m-1}+1}} \end{align*}
이를 통해 아래 다항식을 만들 수 있다.
q(x)=(z1−x)(z2−x)⋯(zm−1−x).q(x)=(z_1-x)(z_2-x)\cdots(z_{m-1}-x).
m<n+2m<n+2를 가정했으므로 m−1<nm-1<n을 만족하기 때문에 q(x)∈Pnq(x)\in\mathcal{P}_n가 된다.
다음은 p+λq∈Pnp+\lambda q \in \mathcal{P}_n가 f(x)f(x)에 대해 p(x)p(x)보다 더 최적근사함수임을 보일것이다.
q(x)q(x)는 (±\pm)intervals에서 0이 아니므로 f−pf-p와 같은 부호를 가진다. 따라서 I1,I2,⋯ ,Ik1I_1,I_2,\cdots, I_{k_1} 에서 (z−x)>0(z-x)>0이므로 q>0q>0다. 마찬가지로 Ik1+1,Ik1+2,⋯ ,Ik2I_{k_1+1},I_{k_1+2},\cdots,I_{k_2} 에서 (z−x)<0(z-x)<0이므로 q<0q<0다.
다음은 λ\lambda를 찾을 것이다. ϵ=max⁡x∈N∣f(x)−p(x)∣\epsilon=\max_{x\in N}{|f(x)-p(x)|}라 한다. 정의에 의해서 ϵ<E\epsilon<E가 성립한다. λ>0\lambda>0이라 잡으면 λ∣∣q∣∣<min⁡{E−ϵ,E2}\lambda||q|| < \min\{E-\epsilon, \frac{E}{2}\}가 된다.
다음 단계로 q(x)q(x)가 p(x)p(x)보다 f(x)f(x)에 더 최적근사함수임을 보인다. 이를 위해 x∈Nx\in N일 때와 x∉Nx\notin N일 경우를 나눠서 진행한다.
만약 x∈Nx\in N라면 삼각부등식에 의해 아래 수식이 성립한다.
∣f(x)−(p(x)+λq(x))∣≤∣f(x)−p(x)∣+λ∣q(x)∣≤ϵ+λ∣∣q∣∣∞<E,\begin{align*} |f(x)-(p(x)+\lambda q(x))| &\le |f(x)-p(x)| + \lambda |q(x)|\\ &\le \epsilon + \lambda ||q||_{\infty} < E, \end{align*}
만약 x∉Nx\notin N라면 xx는 (++)interval 또는 (−-)interval이다. 위 수식 4.1에 의해서 ∣f−p∣>E2>λ∣∣q∣∣∞|f-p| > \frac{E}{2} > \lambda ||q||_{\infty}가 성립한다. 그러므로 f−pf-p와 λg(x)\lambda g(x)는 같은부호를 가지게 된다. q(x)q(x)가 SS위에서 00이 아니므로 아래 식이 성립한다.
∣f−(p+λq)∣=∣f−p∣−λ∣q∣≤ϵ+λ∣∣q∣∣∞<E\begin{align*} |f-(p+\lambda q)|&=|f-p|-\lambda|q| \\ &\le \epsilon + \lambda||q||_{\infty} < E \end{align*}
결국f(x)f(x)에 대해 p+λqp + \lambda q가 p(x)p(x)보다 더 최적화된 근사함수이므로 p(x)p(x)가 최적근사함수라는 가정에 모순된다. 그러므로 m<n+2m<n+2는 거짓이기 때문에 m≥n+2m \ge n+2가 성립한다.

4.2 Uniqueness

Theorem 3.

f(x)∈C[a,b]f(x) \in C[a,b] 일 때 f(x)f(x)에 최적근사 nn차 다항식 p(x)p(x)는 유일하게 존재한다.
Proof. Pn\mathcal{P}_n에서 f(x)f(x)에서 최적근사함수가 p(x)p(x)와 q(x)q(x) 두 개 존재한다고 가정하자. 이 때 p(x),q(x)∈Pnp(x),q(x)\in \mathcal{P}_n가 서로 같음을 보일것이다.
만약 두 다항식 모두 최적근사함수라면 ∣∣f−p∣∣∞=∣∣f−q∣∣∞=E||f-p||_{\infty}=||f-q||_{\infty}=E를 만족한다. 또한 두 함수의 평균 r(x)=p+q2r(x)=\frac{p+q}{2} 또한 f−r=f−(p+q2)=(f−p2)+(f−q2)f-r=f-\big(\frac{p+q}{2}\big)=\big(\frac{f-p}{2}\big)+\big(\frac{f-q}{2}\big)이므로 최적근사함수가 된다. 따라서 ∣∣f−r∣∣∞=E||f-r||_{\infty}=E가 성립한다.
Theorem 2에 의해 f−rf-r은 n+2n+2개의 alternating set x0,x1,⋯ ,xn+1x_0,x_1,\cdots,x_{n+1}를 갖는다.
각 ii에 대해
(f−r)(xi)=±E2(f−r)(xi)=(2f−2r)(xi)=±2E(2f−2r)(xi)=(2f−(p+q))=(f−p)(xi)+(f−q)(xi)=±2E∴(f−p)(xi)+(f−q)(xi)=±2E\begin{align*} (f-r)(x_i)=\pm E\\ 2(f-r)(x_i)=(2f-2r)(x_i)=\pm2E\\ (2f-2r)(x_i)=(2f-(p+q))=(f-p)(x_i)+(f-q)(x_i)=\pm2E \\ \therefore(f-p)(x_i)+(f-q)(x_i)=\pm2E \end{align*}
가 성립하고 −E≤(f−p)(xi),  (f−q)(xi)≤E-E\le (f-p)(x_i),\;(f-q)(x_i)\le E가 성립하기 때문에 위 식이 성립하기 위해선
(f−p)(xi)=(f−q)(xi)=±E(f-p)(x_i)=(f-q)(x_i)=\pm E
가 성립해야 한다. 따라서 x0,x1,⋯ ,xn+1x_0,x_1,\cdots,x_{n+1}은 f−rf-r에서 뿐 만 아니라 f−pf-p와 f−qf-q에서도 alternating set이 되어야 한다.
따라서 다항식 q−p=(f−p)−(f−q)q-p=(f-p)-(f-q)는 n+2n+2의 해를 가진다. 그러나 q−p∈Pnq-p\in\mathcal{P}_n이므로 q−pq-p는 최대 nn차 다항식이므로 최대 nn개 해를 가져야한다. 이를 만족하는 nn차 다항식은 없으므로 p(x)=q(x)p(x)=q(x)가 되며 최종적으로 최적근사함수는 유일하게 존재한다.

Theorem 4.

f(x)∈C[a,b]f(x)\in C[a,b]이고 p(x)∈Pnp(x)\in\mathcal{P}_n이라 하자. 만약 f−pf-p가 n+2n+2개 이상의 alternating set을 포함하고 있다면 p(x)p(x)는 Pn\mathcal{P}_n에서 f(x)f(x)의 최적근사함수이다.
Proof. 귀류법을 통해 증명한다. 만약 q(x)q(x)가 p(x)p(x)보다 f(x)f(x)의 더 좋은 최적근사함수라면 p(x)p(x)와 q(x)q(x)는 서로 같다는 과정을 진행할 것이다.
그러므로 x0,x1,⋯ ,xn+1x_0,x_1,\cdots,x_{n+1}가 f−pf-p의 alternating set이라 하고 q(x)∈Pnq(x)\in\mathcal{P}_n가 f(x)f(x)보다 더 최적근사함수라고 가정한다. 그러므로 ∣∣f−q∣∣∞<∣∣f−p∣∣∞||f-q||_{\infty}<||f-p||_{\infty}가 성립한다.
∣f(xi)−p(xi)∣=∣∣f−p∣∣∞>∣∣f−q∣∣∞≥∣f(xi)−q(xi)∣.|f(x_i)-p(x_i)|=||f-p||_{\infty}>||f-q||_{\infty}\ge|f(x_i)-q(x_i)|.
∣f(xi)−p(xi)∣=∣∣f−p∣∣∞|f(x_i)-p(x_i)|=||f-p||_{\infty}은 xix_i가 f−pf-p의 alternating set이므로 성립한다. 또한 xix_i가 f−qf-q에서 alternating set인진 모르지만 ∣f(xi)−q(xi)∣|f(x_i)-q(x_i)|가 f−qf-q의 uniformuniform-norm(max⁡\max 함수)인 ∣∣f−q∣∣∞||f-q||_{\infty}보단 작을것이므로 위 부등식이 성립한다. 위 부등식을 통해 최종적으로 ∣f(xi)−p(xi)∣>∣f(xi)−q(xi)∣|f(x_i)-p(x_i)|>|f(x_i)-q(x_i)|가 성립하게 된다.

lemma 4.1

∣a∣>∣b∣|a|>|b|가 성립하면 aa와 a−ba-b는 같은 부호를 갖는다.
이를 위 부등식에 적용하면 f(xi)−p(xi)f(x_i)-p(x_i)와 f(xi)−p(xi)−f(xi)+q(xi)=q(xi)−p(xi)f(x_i)-p(x_i)-f(x_i)+q(x_i)=q(x_i)-p(x_i)가 같은 부호를 갖게 된다. f−pf-p가 같은 부호를 가지므로 q−p=(f−p)−(f−q)q-p=(f-p)-(f-q) 또한 n+2n+2번 이상 부호를 바꾸는 함수가 되며 이는 즉, q−pq-p가 최소 n+1n+1개의 해를 가짐을 말한다. 이 때, q−p∈Pnq-p\in \mathcal{P}_n이므로 n+1n+1개 이상의 해를 갖기 위해선 q(x)=p(x)q(x)=p(x)여야 한다. 이는 위에서 가정한 ∣∣f−q∣∣∞<∣∣f−p∣∣∞||f-q||_{\infty}<||f-p||_{\infty}에 모순되므로 p(x)p(x)는 Pn\mathcal{P}_n에서 f(x)f(x)의 최적근사함수이다.
위 Theorem 2와 Theorem 4를 합치면 아래와 같이 두 명제가 서로 필요충분 조건이 된다.
f(x)∈C[a,b]f(x)\in C[a,b]이고 p(x)∈Pnp(x)\in\mathcal{P}_n이라 하자. f−pf-p가 n+2n+2개 이상의 alternating set을 포함하고 있다⇔\Leftrightarrow p(x)p(x)는 Pn\mathcal{P}_n에서 f(x)f(x)의 최적근사함수이다.
결론적으로 f−pf-p는 적어도 n+1n+1개 이상의 해를 갖는다.

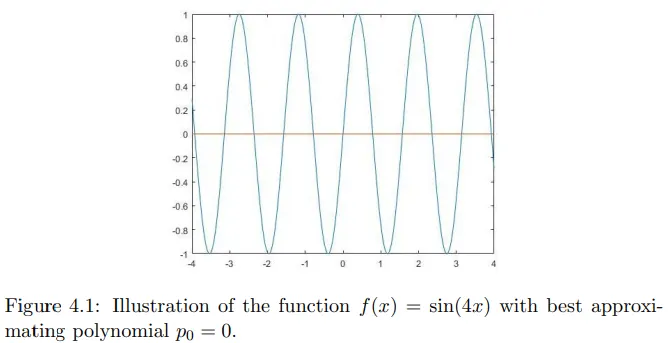
Example 1.

폐구간 [−π,π][-\pi,\pi]에서 함수 f(x)=sin⁡(4x)f(x)=\sin{(4x)}가 있다고 하자. 아래 그림은 이 때 최적근사함수는 p0=0p_0=0이 된다는 것을 보여준다.
손실값 E=f−p=sin⁡(4x)E=f-p=\sin(4x)은 [−π,π][-\pi,\pi]에서 8개의 다른 alternating set을 가지게 된다. 8개의 alternating set을 가지고 있으므로 Theorem 2와 Theorem 4에 의해 p0=p1=p2=p3=p4=p5=p6=0p_0=p_1=p_2=p_3=p_4=p_5=p_6=0이 최적근사함수가 된다. 즉, n+2=8n+2=8 까진 최적근사함수 nn차 다항식 pn=0p_n=0이 된다. 따라서 p7p_7은 n+2=7+2=9n+2=7+2=9개 이상의 alternating set이 있어야 최적근사함수이므로 p7=0p_7=0이 아니다. 따라서 P7\mathcal{P}_7에선 p7=0p_7=0보다 더 좋은 최적근사함수가 존재한다.

Example 2.

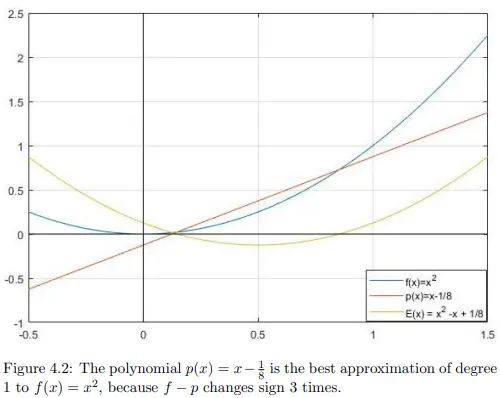
f(x)=x2f(x)=x^2의 선형 최적근사함수는 p=x−18p=x-\frac{1}{8}을 보일것이다(최적근사함수를 찾는법은 6장에서 배우므로 여기선 넘어간다).
선형이므로 최적근사함수의 차수 n=1n=1이다. 따라서 f−pf-p는 적어도 2+1=32+1=3번 부호가 바뀌어야 한다. 결국 f−pf-p는 적어도 2개의 해를 갖게 된다. 즉, 아래 그림과 같이 f-p는 부호가 3번 바뀌고 2개의 해: x=12±142x=\frac{1}{2}\pm\frac{1}{4}\sqrt{2}를 가진다.
본 과정들을 통해 최적근사 다항식의 특징을 알았으므로 다음단계는 f(x)f(x)와 최적근사함수 p(x)p(x)의 최대손실값을 찾을것이다. 이를 드라발레 푸생이란 수학자가 아래 Theorem을 통해 손실값 EE의 하한값을 증명하는 법을 제시하였다.

Theorem 5 (드라발레 푸생)

f(x)∈C[a,b]f(x)\in C[a,b]고 f(xi)−q(xi)f(x_i)-q(x_i)에서 n+2n+2개의 점a≤x0<x1<⋯<xn+1≤ba\le x_0 < x_1 < \cdots < x_{n+1} \le b에서 부호가 바뀌는 q(x)∈Pnq(x)\in\mathcal{P}_n가 존재한다고 하자. 이 때 아래 식이 성립한다.
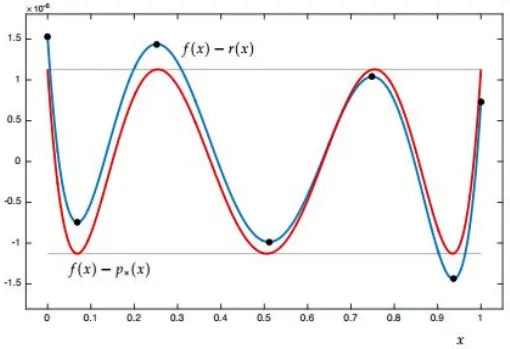
E=min⁡p∈Pn∣∣f−p∣∣∞≥min⁡i=0,⋯ ,n+1∣f(xi)−q(xi)∣.E=\min_{p\in\mathcal{P}_n}||f-p||_{\infty}\ge \min_{i=0,\cdots,n+1}|f(x_i)-q(x_i)|.
이 Theorem을 증명하기 전에 밑에 그림을 참고하여 어떻게 이 Theorem이 동작하는지 확인한다.
만약 함수 f(x)=exf(x)=e^x에 5차다항식(quintic polynomial)을 최적화 한다고 하자. 아래 그림은 5차 다항식 r(x)∈P5r(x)\in\mathcal{P}_5가 f−rf-r이 7번 부호가 바뀌게 함을 보인다. 이 때 r(x)r(x)는 최적근사함수는 아니다. 붉은색 곡선은 최적근사함수 p(x)p(x)의 오차를 보여주며 7개의 점에서 오차의 부호가 바뀐다.
f(x)−r(x)f(x)-r(x)의 부호가 n+2n+2번 바뀌었기 떄문에 부호를 바꾸는 어떤 점 xix_i에서 오차 ±∣∣f−p∣∣∞\pm||f-p||_{\infty}는 ∣f(xi)−r(xi)∣|f(x_i)-r(x_i)|를 초과한다.
드라발레 푸셍의 이론은 ∣∣f−p∣∣∞||f-p||_{\infty}의 하한을 결정하는데 좋은 매커니즘을 제공한다.
Proof. 귀류법을 통해 증명한다. 이를 위해 부등식이 성립하지 않는다고 가정하면 최적근사함수 p(x)p(x)는 아래 부등식을 만족한다.
max⁡0≤i≤n+1∣f(xi)−p(xi)∣≤E<min⁡0≤i≤n+1∣f(xi)−q(xi)∣\max_{0\le i \le n+1}{|f(x_i)-p(x_i)|} \le E < \min_{0 \le i \le n+1}{|f(x_i)-q(x_i)|}
∣f(xi)−p(xi)∣|f(x_i)-p(x_i)|의 최대값이 ∣f(xi)−q(xi)∣|f(x_i)-q(x_i)|의 최소값보다 작으므로 아래 식이 성립한다.
∣f(xi)−p(xi)∣<∣f(xi)−q(xi)∣,        for  all    i=0,⋯ ,n+1|f(x_i)-p(x_i)|<|f(x_i)-q(x_i)|, \;\;\;\;\mathbf{for\;all}\;\;i=0,\cdots,n+1
p(x),q(x)∈Pnp(x),q(x)\in\mathcal{P}_n이므로 아래와 같이 정리할 수 있다.
p(x)−q(x)=(f(x)−q(x))−(f(x)−p(x))p(x)-q(x)=(f(x)-q(x))-(f(x)-p(x))
f(xi)−q(xi)f(x_i)-q(x_i)의 크기가 f(xi)−p(xi)f(x_i)-p(x_i)의 크기보다 항상 크기 때문에 이를 lemma 4.1을 이용하면 f(xi)−q(xi)f(x_i)-q(x_i)의 부호가 f(xi)−q(xi)−(f(xi)−p(xi))=p(xi)−q(xi)f(x_i)-q(x_i)-(f(x_i)-p(x_i))=p(x_i)-q(x_i)와 항상 같게 된다. 정리하면
sgn(p(xi)−q(xi))=sgn(f(xi)−q(xi))sgn(p(x_i)-q(x_i))=sgn(f(x_i)-q(x_i))
가 성립한다 (sgnsgn은 부호를 구하는 함수다).
부호가 바뀌는 점이 n+2n+2개 존재한다고 했고 이는 해가 n+1n+1개 존재하는 것을 의미한다. 그러나 nn차 다항식에서 n+1n+1개의 해를 가지려면 00이 되는 방법밖에 없다. 따라서 p(x)=q(x)p(x)=q(x)여야 하며 이는 모순이므로 적어도 한개의 ii에선 En(f)≥∣f(xi)−q(xi)∣E_n(f) \ge |f(x_i)-q(x_i)|가 성립한다.