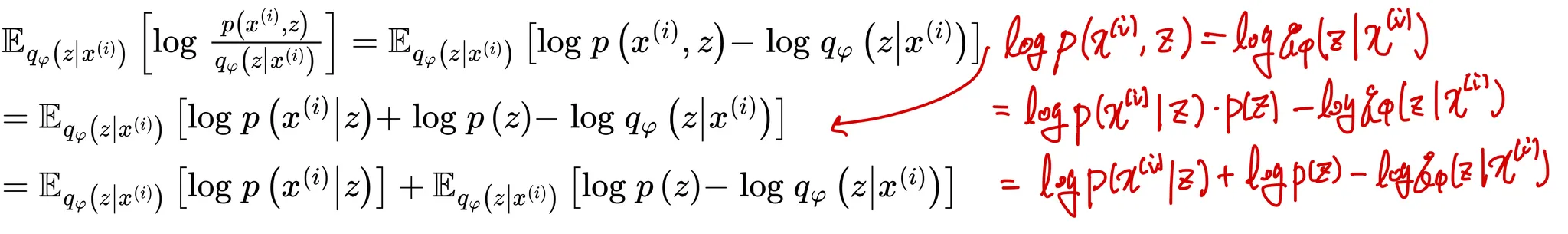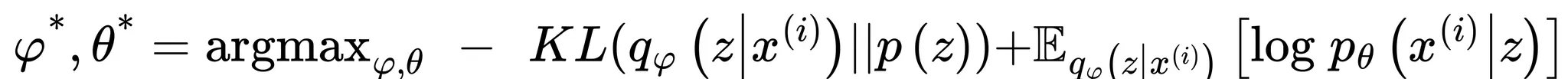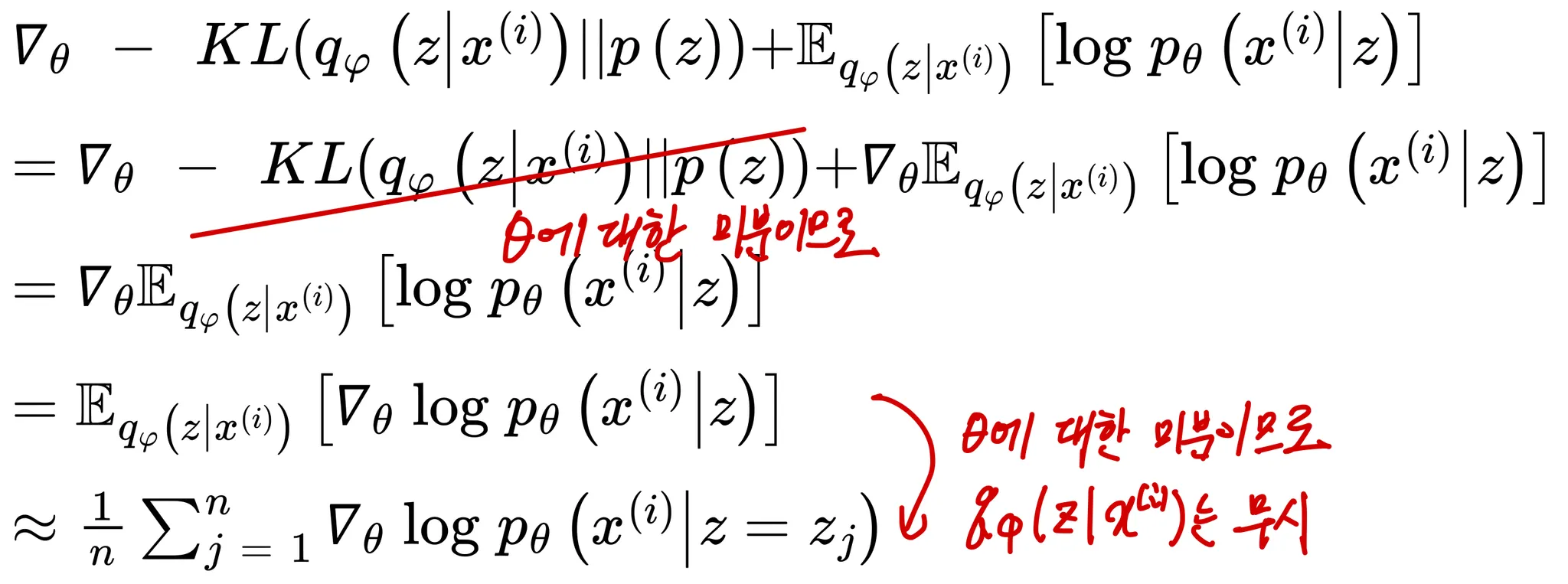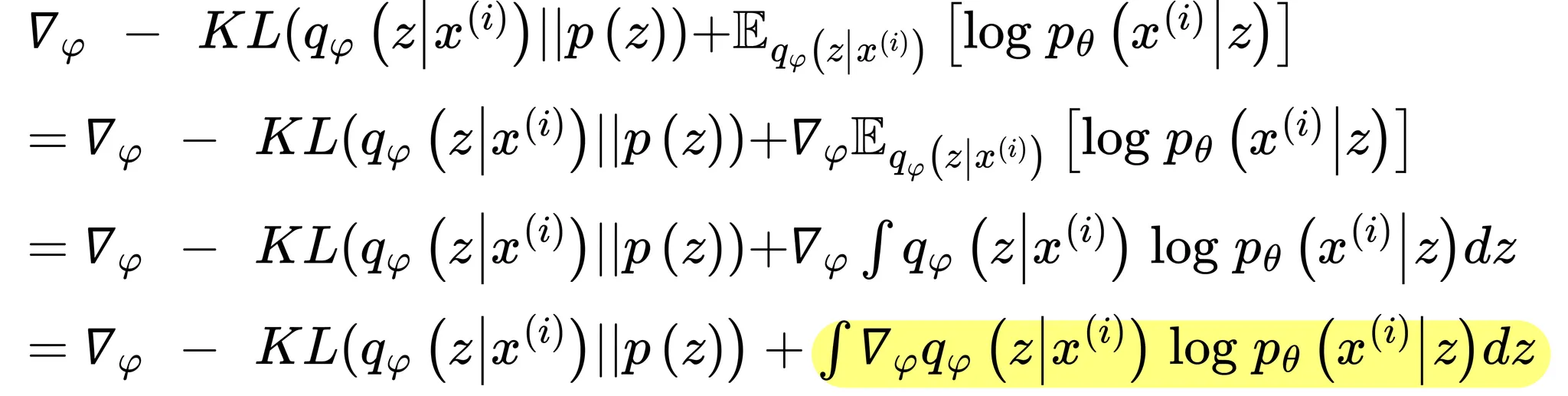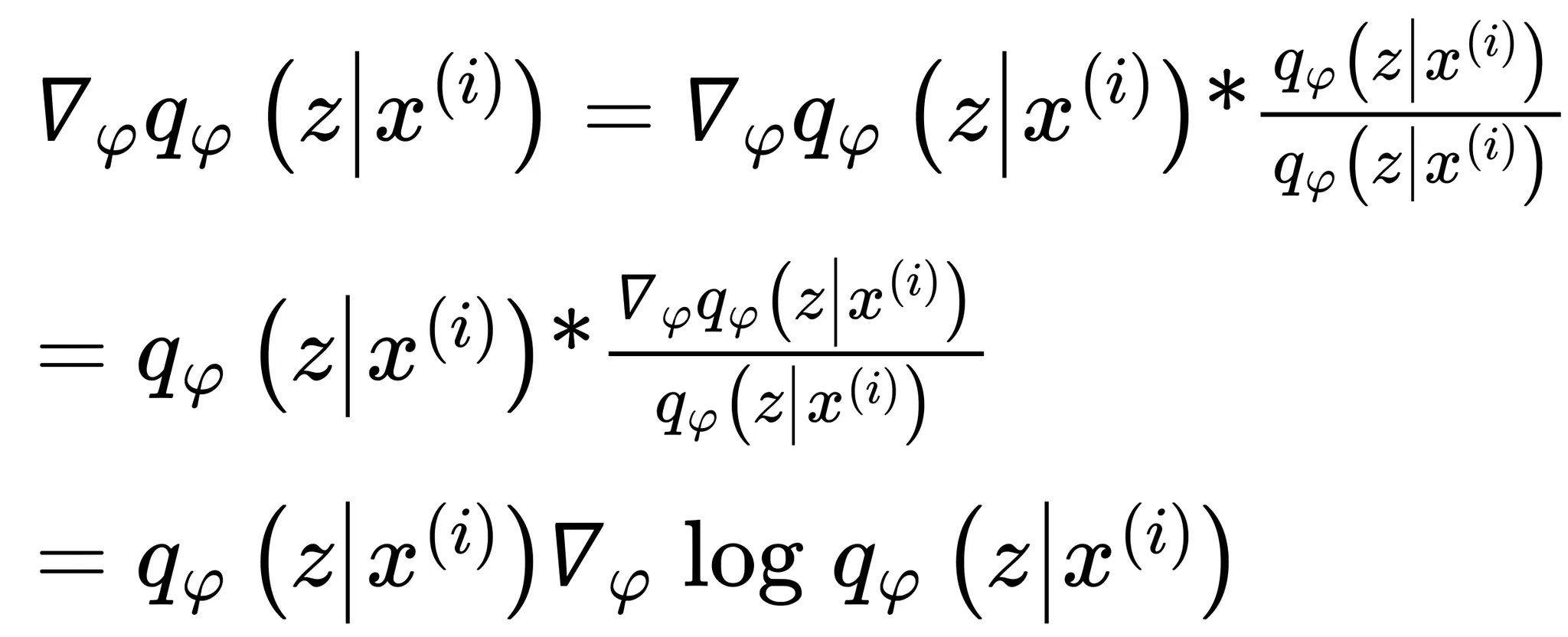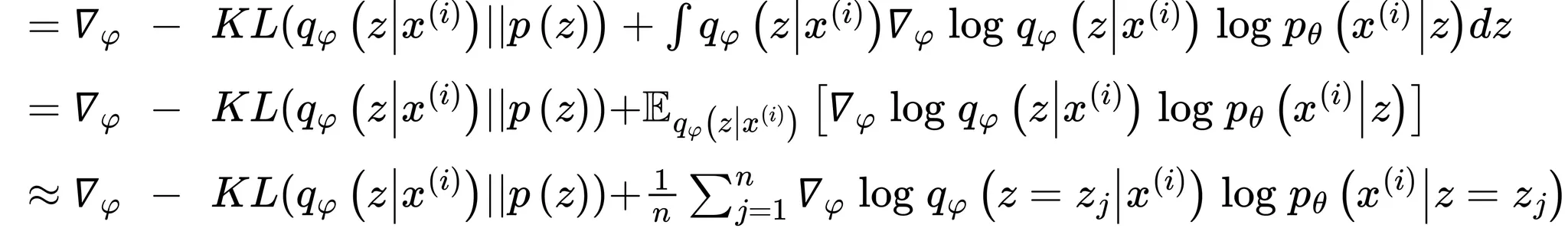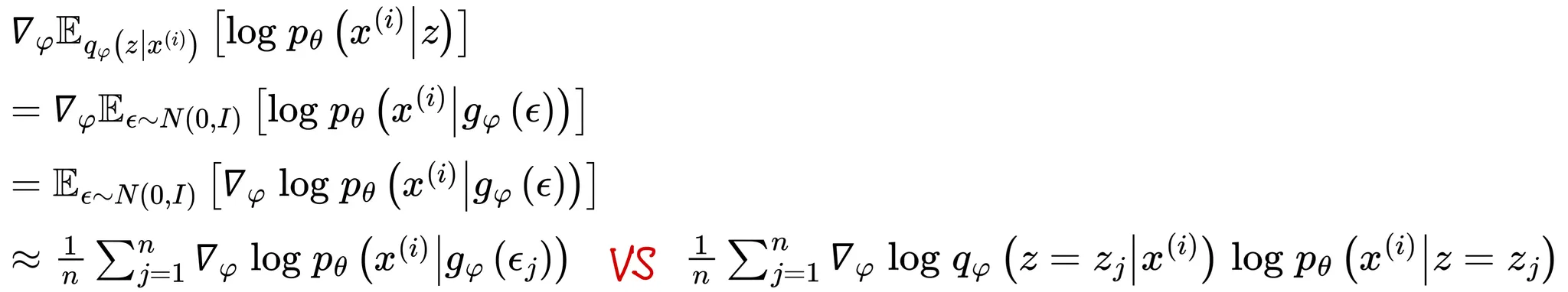📄

Variational Autoencoders (VAE)

•

VAE는 뉴럴넷으로 잠재변수 zzz와 관측된 데이터 xxx사이의 관계를 학습

•

잠재변수가 주어졌을 때 데이터에 대한 분포를 출력으로 가지는 네트워크를 decoder라 하며 pθ(x∣z)p_\theta(x|z)pθ​(x∣z)로 표현하며 θ\thetaθ는 뉴럴넷의 가중치를 의미

•

θ\thetaθ를 최적화 하여 p(x∣z)p(x|z)p(x∣z)를 실제 분포에 가까워지도록 학습

•

zzz의 사후분포(posterior)인 p(z∣x)p(z|x)p(z∣x)를 뉴럴넷으로 엔코딩하며 이를 행하는 네트워크를 encoder라고 하고 qφ(z∣x)q_{\varphi}(z|x)qφ​(z∣x)로 표현

•

실제 사후분포에 가깝도록 encoder의 파라미터 φ\varphiφ를 최적화

•

본 챕터에선 VAE를 위한 두가지 효율적인 방법인 ELBO와 reparametrization을 소개

Evidence Lower Bound (ELBO)

•

encoder와 decoder의 파라미터를 최적화하기 위해 수식을 튜닝하는 방식으로 데이터분포 p(x)p(x)p(x)의 하한을 활용

•

임의의 관측데이터 xxx의 원소를 x(i)x^{(i)}x(i)라 하고 데이터를 생성하는 잠재변수 zzz가 존재한다고 가정

•

우린 잠재변수의 사후확률 p(z∣x(i))p(z|x^{(i)})p(z∣x(i))가 존재한다는것은 알고 있으나 어떤분포인진 알 수 없으므로 이 분포가 어떤 잠재변수의 분포 qφ(z∣x(i))q_\varphi(z|x^{(i)})qφ​(z∣x(i))로 근사할 수 있다고 가정

•

이때 qqq는 최적화를 쉽게 할 수 있어야하며 동시에 실제 사후확률을 정확하게 모델링 할 수 있을정도론 복잡도가 높아야 하므로 이를 뉴럴넷으로 설계

•

x(i)x^{(i)}x(i)의 확률인 p(x(i))p(x^{(i)})p(x(i))를 바로 사용하지 않고 최적화를 좀 더 편하게 하기 위해 log⁡p(x(i))\log p(x^{(i)})logp(x(i))를 최적화하면 아래와 같이 전개

\begin{align*} &p(x^{(i)},z)=p(x^{(i)})\cdot p(z|x^{(i)}) \\ &\therefore p(x^{(i)})=\frac{p(x^{(i)},z)}{p(z|x^{(i)})} \\ & \log p(x^{(i)})=\log \frac{p(x^{(i)},z)}{p(z|x^{(i)})}=\log p(x^{(i)},z)-\log p(z|x^{(i)}) \\ &= \log p(x^{(i)},z)-\log p(z|x^{(i)}) +\log q_{\varphi}(z|x^{(i)}) - \log q_{\varphi}(z|x^{(i)}) \end{align*}

•

좌변인 log⁡p(x(i))\log p(x^{(i)})logp(x(i))은 상수이므로 양변에 Expectation 연산을 취해도 똑같으므로 양변에 Expectation 연산을 취하여 전개

\begin{align*} &\log p(x^{(i)}) \\ &=\mathbb{E}_{q_\varphi(z|x^{(i)})}[\log p(x^{(i)},z)-\log p(z|x^{(i)}) +\log q_{\varphi}(z|x^{(i)}) - \log q_{\varphi}(z|x^{(i)})] \\ &=\mathbb{E}_{q_\varphi(z|x^{(i)})}[\log p(x^{(i)},z)- \log q_{\varphi}(z|x^{(i)}) +\log q_{\varphi}(z|x^{(i)})-\log p(z|x^{(i)}) ] \\ &=\mathbb{E}_{q_\varphi(z|x^{(i)})}\bigg[\log{\frac{p(x^{(i)},z)}{q_{\varphi}(z|x^{(i)})}}\bigg] + \mathbb{E}_{q_\varphi(z|x^{(i)})}\bigg[\log{\frac{q_{\varphi}(z|x^{(i)})}{p(z|x^{(i)})}}\bigg] \\ &=\mathrm{ELBO} +\mathrm{KL}(q_{\varphi}(z|x^{(i)}) || p(z|x^{(i)})) \end{align*}

•

우리는 잠재변수의 분포 p(z∣x(i))p(z|x^{(i)})p(z∣x(i))와 이를 근사하는 분포 qφ(z∣x(i))q_\varphi(z|x^{(i)})qφ​(z∣x(i))의 거리가 최소화되어야 하므로 KL(qφ(z∣x(i))∣∣p(z∣x(i)))\mathrm{KL}(q_{\varphi}(z|x^{(i)}) || p(z|x^{(i)}))KL(qφ​(z∣x(i))∣∣p(z∣x(i)))를 최대화 시켜야함

•

이 때 log⁡p(x(i))\log p(x^{(i)})logp(x(i))는 상수이므로 KL\mathrm{KL}KL을 최대화 시키는것은 ELBO\mathrm{ELBO}ELBO를 최소화 시키는것과 같고 이를 이용하면 아래와 같이 ELBO\mathrm{ELBO}ELBO를 전개할 수 있음

•

앞에서 언급한것과 같이 p(z∣x(i))p(z|x^{(i)})p(z∣x(i))는 모르므로 qφ(z∣x(i))q_\varphi(z|x^{(i)})qφ​(z∣x(i))로 근사하여 변형하면 아래와 같은 최종 최적화 수식을 얻을 수 있음

•

먼저 위 식을 최대화 하는 θ∗\theta^{*}θ∗를 구하기 위해 θ\thetaθ에 대해 미분하면 아래와 같이 전개됨

•

φ∗\varphi^{*}φ∗ 또한 같은 방법으로 아래와 같이 전개함

•

θ∗\theta^{*}θ∗를 구할 때와 달리 φ∗\varphi^{*}φ∗의 경우 위 형광색으로 표시한 ∫▽φqφ(z∣x(i))log⁡pθ(x(i)∣z)dz\int \triangledown_{\varphi}q_\varphi(z|x^{(i)})\log p_\theta (x^{(i)}|z)dz∫▽φ​qφ​(z∣x(i))logpθ​(x(i)∣z)dz를 구하기가 까다로움

•

이를 위해 로그트릭(▽θ  p(τ∣θ)=p(τ∣θ)▽θlog⁡p(τ∣θ)\triangledown_\theta\;p(\tau|\theta)=p(\tau|\theta)\triangledown_\theta\log p(\tau|\theta)▽θ​p(τ∣θ)=p(τ∣θ)▽θ​logp(τ∣θ))을 사용하여 
▽φqφ(z∣x(i))=qφ(z∣x(i))▽φlog⁡qφ(z∣x(i))\triangledown_{\varphi}q_\varphi(z|x^{(i)})=q_\varphi(z|x^{(i)})\triangledown_{\varphi}\log q_\varphi(z|x^{(i)})▽φ​qφ​(z∣x(i))=qφ​(z∣x(i))▽φ​logqφ​(z∣x(i))라 할 수있고 
정리하면 ▽φlog⁡qφ(z∣x(i))=▽φqφ(z∣x(i))qφ(z∣x(i))\triangledown_{\varphi}\log q_\varphi(z|x^{(i)})=\frac{\triangledown_{\varphi}q_\varphi(z|x^{(i)})}{q_\varphi(z|x^{(i)})}▽φ​logqφ​(z∣x(i))=qφ​(z∣x(i))▽φ​qφ​(z∣x(i))​가 됨

•

이를통해  ▽φqφ(z∣x(i))\triangledown_{\varphi}q_\varphi(z|x^{(i)})▽φ​qφ​(z∣x(i))를 아래와 같이 전개할 수 있음

•

위 식을 다시 위의 ▽φ\triangledown_{\varphi}▽φ​를 구하기 위한 식에 대입하면 아래와 같이 전개할 수 있음

Reparametrization trick

•

φ\varphiφ과 관련한 미분값이 낮은분산값을 가지도록 계산하기 위해 Reparametrization trick을 활용

•

zzz가 encoder에 의해 생성되므로 다양한 zzz값이 만들어지게 되며 이는 결국 encoder의 출력값이자 decoder의 입력값인 zzz가 높은 분산값을 가지게 됨을 의미함

•

decoder에 들어갈 입력값이 배치마다 차이가 커지게 되므로 학습이 잘 안되며 이를 해결하기 위해 배치크기를 늘려 많은 샘플을 만들어 완화시킬 수 있으나 이런 방식은 계산량측면에서 비효율적임

•

즉, 분산이 작은 zzz를 생성해야하며 이를 위해 encoder의 가중치와 상관없는 사후분포(주로 다중가우시안 분포 등) 근사를 활용

•

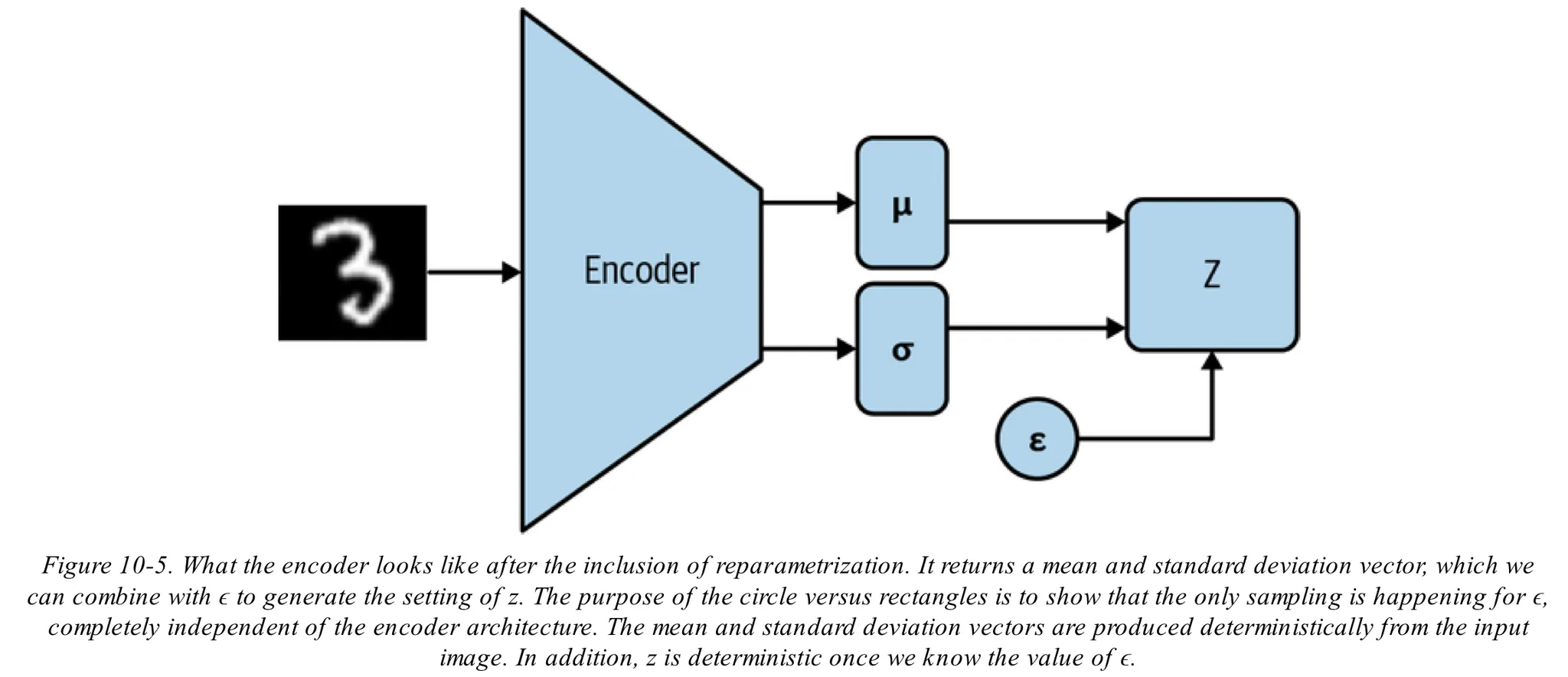
encoder의 출력인 qφ(z∣x(i))q_\varphi(z|x^{(i)})qφ​(z∣x(i))가 분포 N(z;μ^φ,σ^φ2I)N(z;\hat{\mu}_{\varphi}, \hat{\sigma}^2_\varphi I)N(z;μ^​φ​,σ^φ2​I)를 따른다고 가정

•

다중 가우시안분포의 원소를 zi∼N(z;μ^φ,σ^φ2I)z_i\sim N(z;\hat{\mu}_{\varphi}, \hat{\sigma}^2_\varphi I)zi​∼N(z;μ^​φ​,σ^φ2​I)라 할 때 Reparametrization trick를 사용하면 아래와 같이 표현할 수 있음

z\sim N(z;\hat{\mu}_{\varphi}, \hat{\sigma}^2_\varphi I)\Leftrightarrow z=\hat{\mu}_{\varphi}+ \hat{\sigma}_\varphi*\epsilon,\;\epsilon\sim N(0,I)

•

즉, zzz를 gφ(ϵ)=μ^φ+σ^φ∗ϵg_\varphi(\epsilon)=\hat{\mu}_{\varphi}+ \hat{\sigma}_\varphi*\epsilongφ​(ϵ)=μ^​φ​+σ^φ​∗ϵ로 두고 아래와 같이 연산하며 ϵ\epsilonϵ을 보조랜덤변수(auxiliary random variable)라 함

•

이를 통해 encoder의 출력에 바로 의존하지 않고 encoder의 분산과 평균에만 의존하여 출력이 낮은 분산값을 가지도록 유도

•

그러나 본 방식은 사후분포가 가우시안을 따른다는 보장이 없다는 단점을 가짐

전체 코드

# this code is made by chatgpt
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

# VAE 하이퍼파라미터 설정
batch_size = 128
learning_rate = 0.001
epochs = 20
latent_dim = 20

# 데이터 전처리 및 로드
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])

train_dataset = datasets.MNIST(root='./data', train=True, transform=transform, download=True)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)

# VAE 모델 정의
class VAE(nn.Module):
    def __init__(self, latent_dim):
        super(VAE, self).__init__()
        # Encoder
        self.encoder = nn.Sequential(
            nn.Linear(28*28, 400),
            nn.ReLU(),
            nn.Linear(400, 200),
            nn.ReLU(),
        )
        self.fc_mu = nn.Linear(200, latent_dim)
        self.fc_logvar = nn.Linear(200, latent_dim)
        
        # Decoder
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, 200),
            nn.ReLU(),
            nn.Linear(200, 400),
            nn.ReLU(),
            nn.Linear(400, 28*28),
            nn.Sigmoid()
        )
        
    def encode(self, x):
        h1 = self.encoder(x)
        mu = self.fc_mu(h1)
        logvar = self.fc_logvar(h1)
        return mu, logvar
    
    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + std * eps
    
    def decode(self, z):
        return self.decoder(z)
    
    def forward(self, x):
        mu, logvar = self.encode(x)
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar

# 손실 함수 정의
def loss_function(recon_x, x, mu, logvar):
    # 재구성 손실 (Binary Cross Entropy)
    BCE = nn.functional.binary_cross_entropy(recon_x, x, reduction='sum')
    
    # KL 발산 (Kullback-Leibler Divergence)
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return BCE + KLD

# 모델 및 옵티마이저 초기화
model = VAE(latent_dim).cuda()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

# 학습 루프
for epoch in range(epochs):
    model.train()
    train_loss = 0
    for batch_idx, (data, _) in enumerate(train_loader):
        data = data.cuda()
        data = data.view(-1, 28*28)
        
        optimizer.zero_grad()
        recon_batch, mu, logvar = model(data)
        loss = loss_function(recon_batch, data, mu, logvar)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()
        
        if batch_idx % 100 == 0:
            print(f'Epoch [{epoch}/{epochs}] Batch [{batch_idx}/{len(train_loader)}] Loss: {loss.item() / len(data):.6f}')
    
    print(f'====> Epoch: {epoch} Average loss: {train_loss / len(train_loader.dataset):.6f}')

Python

복사

출처

•

Fundamentals of Deep Learning, 2nd Edition by Nithin Buduma, Nikhil Buduma, Joe Papa