Introduction
implicit problem은 입력값으로 공간 또는 시공간의 좌표 , 그리고 해당 좌표에 관한 의 미분값들을 구하는 문제를 푸는 방식으로 설계된다.
이에 따라 입력값 를 특정 값에 맞추기 위해 를 파라미터로 하는 신경망을 학습시키는 것을 목표로 한다. 좀 더 간단한 예시를 들면 일반적인 이미지를 표현하는 것을 함수라 생각하고 표현하면 입력값으로 좌표(x,y)가 주어지면 해당하는 픽셀의 색상(RGB)값을 출력값으로 갖는 함수라 표현할 수 있을 것이다. 이 때 같은 기능을 하는 함수를 신경망으로 설계하게 되면 네트워크의 파라미터 들이 앞서 얘기한 이미지와 동일한 정보를 갖게 된다. 신경망의 파라미터들은 일반적으로 이미지 보다 적은 벡터들로 원본 이미지를 표현할 수 있으므로 계산량에서 이점을 가져가며 뿐 만 아니라 연속(continuous) 이고 미분가능한(differentiable)한 표현이 가능하게 된다. 최종적으로 원본값과 가깝게 세부적인 표현이 가능하면서 해상도에 구애받지 않고 더 효율적으로 메모리를 이용할 수 있는 이점을 가지게 된다.
implicit problem에서 가장 많이 활용하는 방식은 ReLU 기반의 MLPs 모델인데 ReLU의 경우 piecewise linear하기 때문에 이계도 함수가 0이라는 문제를 가지며 결국 신호를 처리할 때 좀 더 세세한 정보를 표현할 순 없게 된다. 하이퍼볼릭탄젠트(tanh)나 소프트플러스(softplus) 함수를 기반으로 할 경우 고차원의 미분를 진행할 수 있기 때문에 이러한 문제는 사라지지만 실제 적용했을 때 낮은 성능을 보이는 문제가 있다. 이에 따라 본 연구에서는 사인커브 기반의 방식을 적용하여 높은 성능을 내는 방식을 제안했다.
Related Work
Implicit neural representation
일반적으로 신경망의 추정(inference)와 생성(generate) 기능을 수행하기 위해 사용된다. 그러나 Implicit Representation 분야의 경우 원본 데이터를 신경망을 통해 표현하는 것을 목적으로 하여 전통적인 방식과는 차이가 있다. 이러한 방식은 보통 최적화(optimization)을 위해 사용되는데 예를 들어 두 개의 같은크기의 이미지를 저장한다고 가정하고 하나는 복잡한 그림, 다른 하나는 몇개의 도형으로 구성된 간단한 그림이 있다고 하자. 그냥 해당 이미지 둘을 처리할 때는 크기가 같으므로 같은 메모리를 사용하지만 신경망을 통해 표현할 경우 단순한 이미지는 훨씬 더 적은 파라미터로 표현이 가능하게 된다. 물론 단순한 2차원 이미지의 경우 다양하고 좋은 압축기술이 존재하므로 큰 이득을 보진 못하지만 3차원의 경우 거대한 크기를 가지고 있기 때문에 3차원 도메인에 적용할 시 많은 이득을 볼 수 있다.
Periodic nonlinearities
Neural DE Solvers
Formulation
본 문제를 해결하기 위한 손실함수는 위와 같다. 는 도메인을 결정하는 함수로 만약 original 이미지를 저장하기 위한 함수만 쓴다면 뒤에 를 다 0으로 만드는 등의 기능을 수행한다. 해당 손실함수를 통해 손실함수 을 최소화 시키는 파라미터 함수 의 파라미터 를 구하게 된다.
본 연구의 경우 활성함수를 사인커브 기반으로 설계하여 아래와 같이 표현하였다.
class SineLayer(nn.Module):
def __init__(self, in_features, out_features, bias=True,
is_first=False, omega_0=30):
super().__init__()
self.omega_0 = omega_0
self.linear = nn.Linear(in_features, out_features, bias=bias)
def forward(self, input):
return torch.sin(self.omega_0 * self.linear(input))
Python
복사
함수 코드
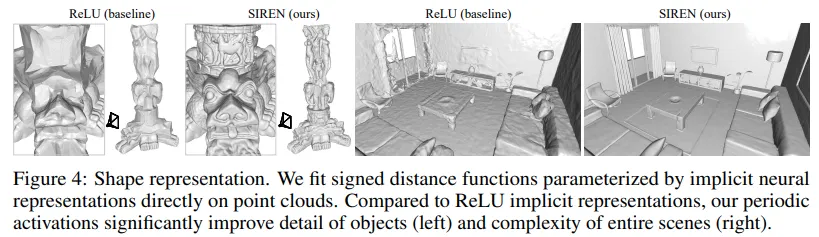
본 연구에서 제시한 SIREN의 경우 높은 정확도를 내면서도 좋은 속도를 보여준다.
Experiments
Solving the Poisson Equation
or
.png&blockId=9c75815d-ddc3-4a09-abf2-5981e8e3bab6)
.png&blockId=be10bfa5-f64b-4236-b9f6-f71c133b128c)