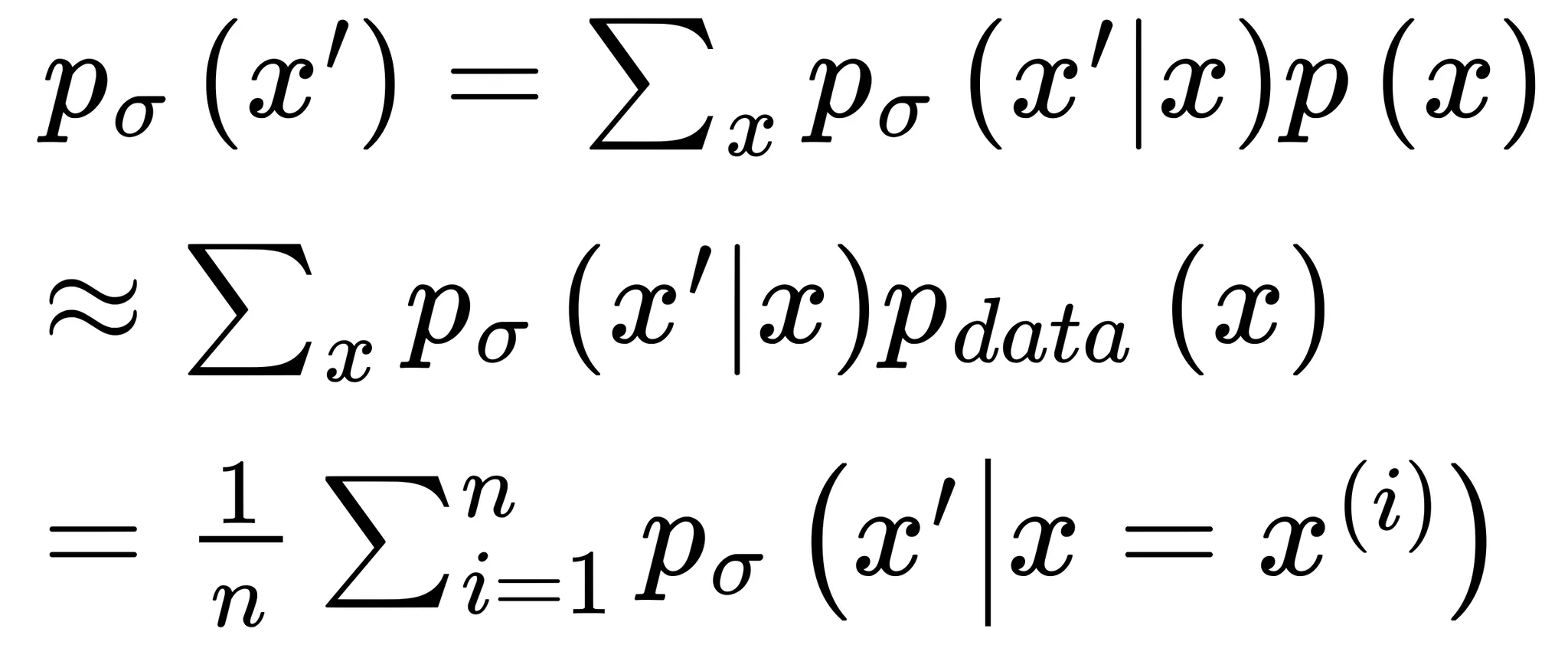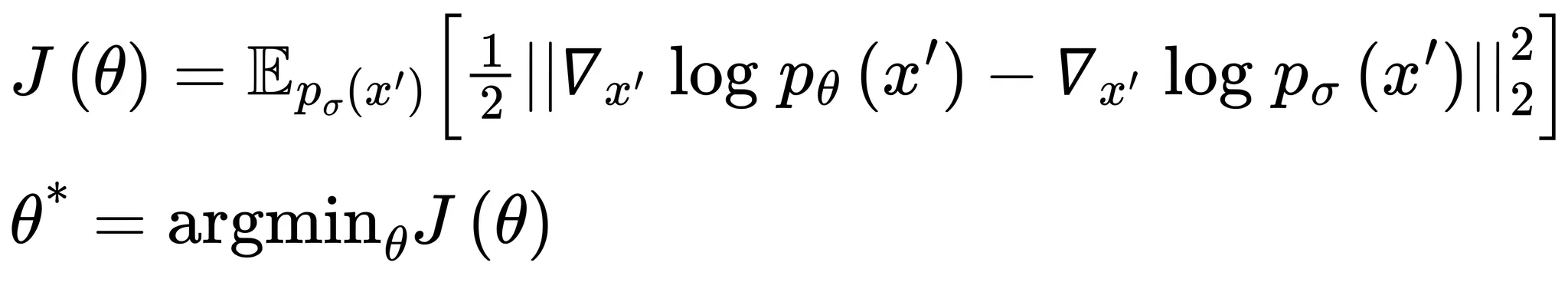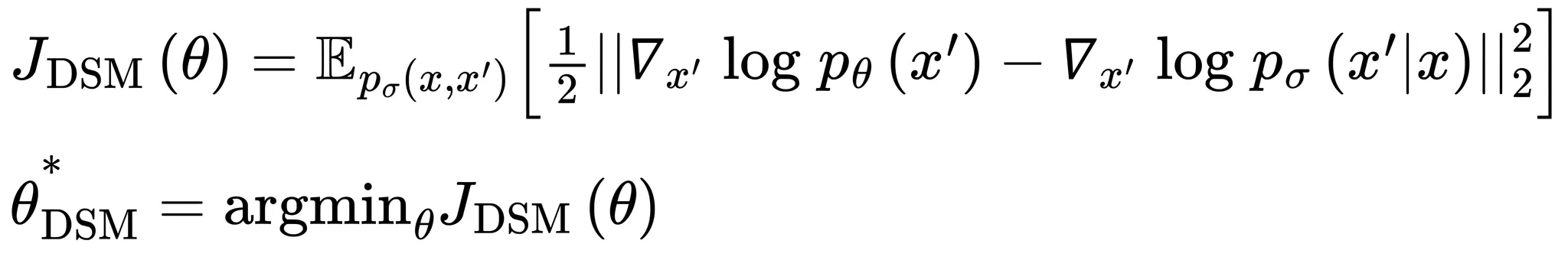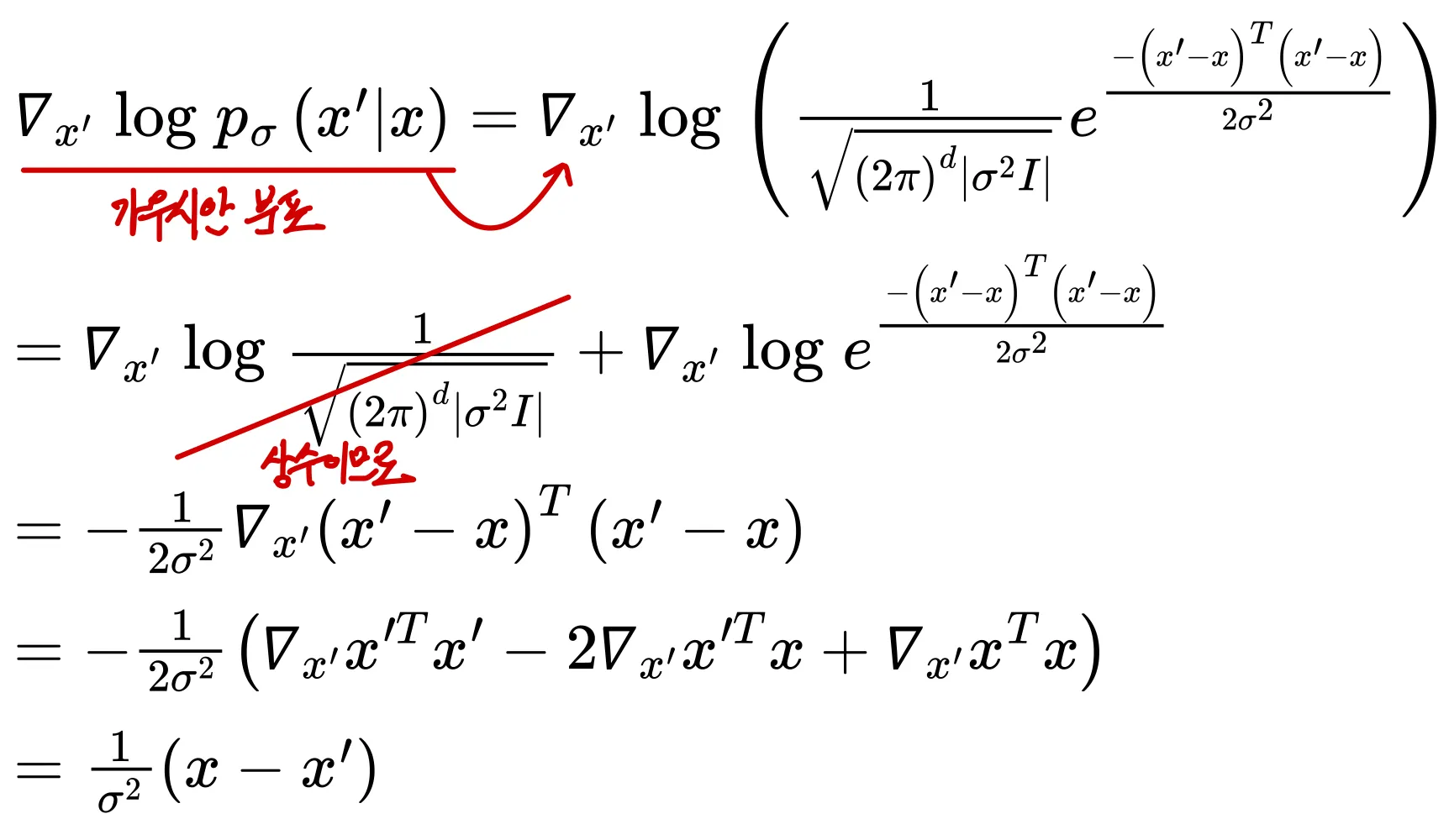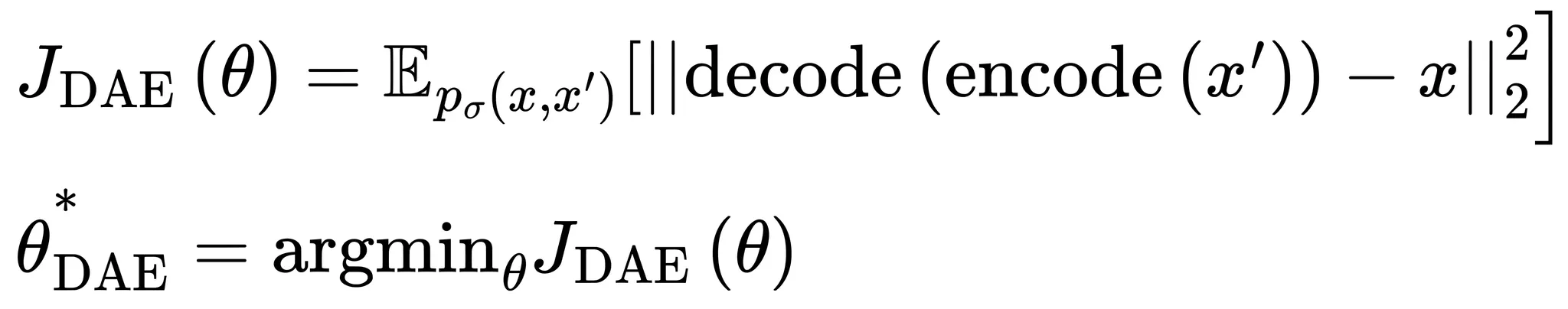•
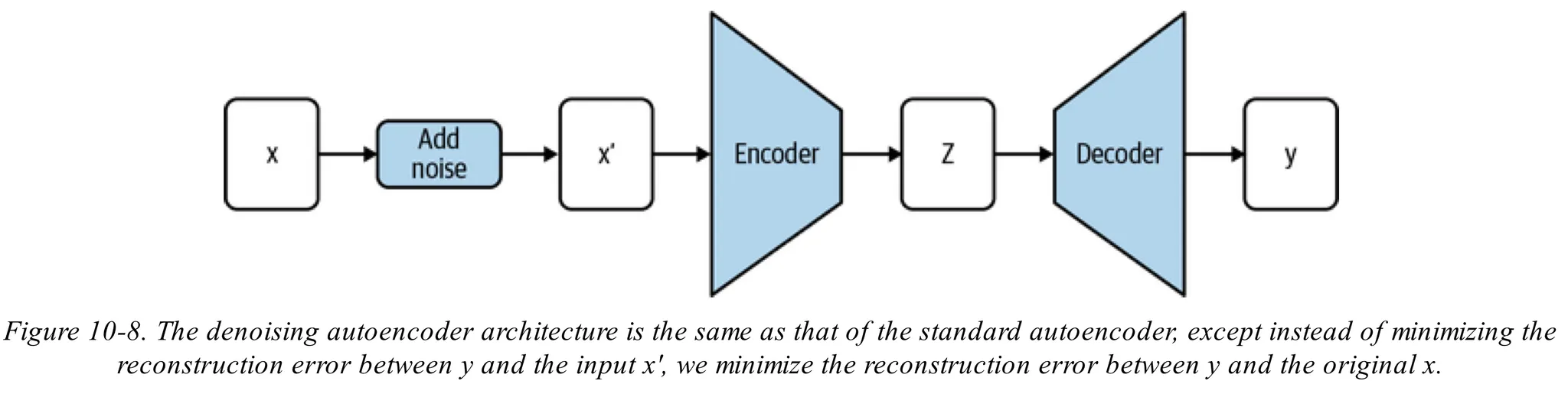
위 그림과 같이 denoising autoencoder는 입력값 에 노이즈를 추가하여 을 만들고 이를 일반적인 AE에 입력값으로 넣고 출력 가 원본입력값 를 복원하도록 학습
•
첫 제안 연구에선 회전이나 배경 노이즈와 같은 다양한 데이터 어그멘테이션을 적용하여 성능을 높였음
Denoising Score Matching
•
원본 이미지에 가우시안 분포를 적용하여 를 구하며 과 는 같은 도메인으로 정의되며 는 가우시안 노이즈의 표준편차를 의미
•
전체 확률의 법칙(law of total probability)에 의해 아래와 같이 정리
•
최적화함수는 아래와 같이 재정의할 수 있음
•
이므로 아래와 같이 미분값을 계산할 수 있음
Denoising Autoencoder
•
denoising score matching와 동일한 최적화함수를 가지며 AE와 동일한 아키텍쳐를 가지나 입력데이터와 훈련손실함수가 다름
•
본 자료에선 생략하나 를 최적화하는것과 을 최적화 하는것이 같으므로 결국 DAE은 DSM을 통해 훈련시킬 수 있음
총 과정 정리
1.
를 최소화하는 방향으로 denoising AE를 학습시킨다.
2.
가 주어졌을 때, 을 통해 점수를 계산
3.
로 부터 을 샘플링
4.
2번과 3번 결과를 Langevin dynamics 방정식에 넣어 다음 샘플 을 구함
5.
을 이용하여 2번부터 4번까지 과정을 반복
출처
•
Fundamentals of Deep Learning, 2nd Edition by Nithin Buduma, Nikhil Buduma, Joe Papa