///
Search
📄

Chapter 5

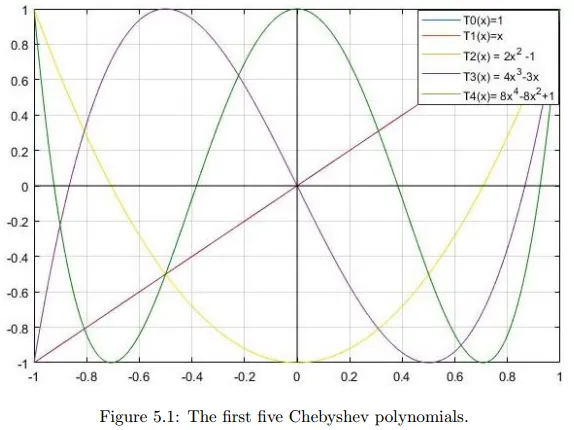
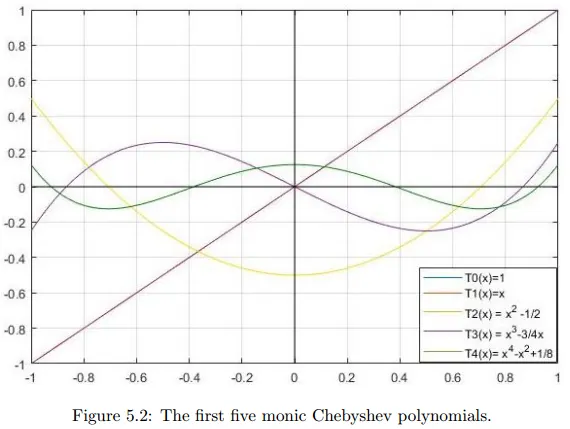
Chebyshev polynomials

어떻게 체비셰프가 최적근사다항식을 찾을 수 있었는지 보이기 위해서 먼저 체비셰프 다항식에 대해 살펴본다. 본 챕터에선 체피셰프 다항식에 대해 설명하고 몇가지 성질(property)들을 확인한다. 이후 6장에서 이 성질들을 활용하여 실제로 체비셰프 다항식을 통해 최적근사함수를 찾아내는 과정을 설명 한다. 본 챕터는 R. L. Burden and J. Douglas Faires의 저서 Numerical Analysis와 N. L. Carothers의 저서 A short course on approximation theory를 참고하여 작성되었다.

Definition 2.

n차식 체비셰프 다항식은 아래와 같은 식으로 정의된다.
Tn(x)=cos⁡(narccos⁡(x)),      for  each      n≥0.T_n(x)=\cos(n\arccos(x)), \;\;\; for \; each \;\;\; n\ge0.
위 식을 좀 더 자세히 살펴보면,
For          n=0:T0(x)=cos⁡(0)=1For          n=1:T1(x)=cos⁡(arccos⁡(x))=x\begin{align*} \mathbf{For}\;\;\;\;\; &n=0 : &T_0(x)&=\cos(0)=1 \\ \mathbf{For}\;\;\;\;\; &n=1 : &T_1(x)&=\cos(\arccos(x))=x \end{align*}
n≥1n\ge 1에 대해서 위 방정식을 θ=arccos⁡(x)\theta=\arccos(x), x=cos⁡(θ)x=\cos(\theta)로 치환하면 아래와 같이 정리된다.
Tn(θ(x))≡Tn(θ)=cos⁡(nθ),          where          θ∈[0,π]T_n(\theta(x))\equiv T_n(\theta)=\cos(n\theta),\;\;\;\;\;\mathbf{where}\;\;\;\;\;\theta\in[0,\pi]
코사인 덧셈법칙을 이용하여 점화식으로 표현할 수 있다. 과정을 진행하면
Tn+1(θ)=cos⁡((n+1)θ)=cos⁡(θ)cos⁡(nθ)−sin⁡(θ)sin⁡(nθ)andTn−1(θ)=cos⁡((n−1)θ)=cos⁡(θ)cos⁡(nθ)+sin⁡(θ)sin⁡(nθ)\begin{align*} &T_{n+1}(\theta)=\cos((n+1)\theta)=\cos(\theta)\cos(n\theta)-\sin(\theta)\sin(n\theta) \\ \mathbf{and}&\\ &T_{n-1}(\theta)=\cos((n-1)\theta)=\cos(\theta)\cos(n\theta)+\sin(\theta)\sin(n\theta) \end{align*}
위 두 식을 더하면
Tn+1(θ)+Tn−1(θ)=2cos⁡(nθ)cos⁡(θ)Tn+1(θ)=2cos⁡(nθ)cos⁡(θ)−Tn−1(θ)Tn+1(θ)=2cos⁡(narccos⁡(x))cos⁡(θ)−Tn−1(θ)=2xcos⁡(narccos⁡(x))−Tn−1(θ)∴Tn+1(X)=2xTn(x)−Tn−1(x)\begin{align*} &T_{n+1}(\theta)+T_{n-1}(\theta)=2\cos(n\theta)\cos(\theta) \\ &T_{n+1}(\theta)=2\cos(n\theta)\cos(\theta) - T_{n-1}(\theta) \\ &T_{n+1}(\theta)=2\cos(n\arccos(x))\cos(\theta)- T_{n-1}(\theta)=2x\cos(n\arccos(x))- T_{n-1}(\theta)\\ &\therefore T_{n+1}(X)=2xT_n(x)-T_{n-1}(x) \end{align*}
로 점화식을 세울 수 있다.
이를 통해 체비셰프 다항식을 아래와 같이 쓸 수 있다.
T0(x)=1T1(x)=xT2(x)=2xT1(x)−T0(x)=2x2−1T3(x)=2xT2(x)−T1(x)=4x3−3xT4(x)=2xT3(x)−T2(x)=8x4−8x2+1⋯Tn+1(x)=2xTn(x)−Tn−1(x)      n≥1\begin{align*} &T_0(x)=1 \\ &T_1(x)=x \\ &T_2(x)=2xT_1(x)-T_0(x)=2x^2-1 \\ &T_3(x)=2xT_2(x)-T_1(x)=4x^3-3x \\ &T_4(x)=2xT_3(x)-T_2(x)=8x^4-8x^2+1 \\ &\cdots \\ &T_{n+1}(x)=2xT_n(x)-T_{n-1}(x) \;\;\;n\ge 1 \end{align*}
n≥1n \ge 1일 경우 Tn(x)T_n(x)의 nn차항의 계수는 2n−12^{n-1}이 됨을 확인할 수 있다.

5.1 체비셰프 다항식의 성질

체비셰프는 많은 흥미로운 성질들을 가진다. 본 문서에선 15가지 성질들을 소개한다.

P1

체비셰프 다항식은 구간 (−1,1)(-1,1)에서 가중함수(weight function) w(x)=(1−x2)−12w(x)=(1-x^2)^{-\frac{1}{2}}에 대하여 직교(orthogonal) 한다.

Proof.

P2

차수 n≥1n \ge 1인 체비셰프 다항식 Tn(x)T_n(x)는 구간 [−1,1][-1,1]에서 아래와 같은 nn개의 심플제로(simple zeros)를 갖는다.
xˉk=cos⁡(2k−12nπ),          for    each      k=1,2,⋯ ,n.\bar{x}_k=\cos\bigg(\frac{2k-1}{2n}\pi\bigg),\;\;\;\;\;\mathbf{for \;\; each}\;\;\;k=1,2,\cdots,n.
심플제로는 중복도(multiplicity)가 1인 근을 말한다. 중복도는 다항방정식이 주어진 점에서 근을 갖는 횟수를 말한다. 예를들어 f(z)=(z−1)(z−2)f(z)=(z-1)(z-2)라 할 때, z0z_0의 중복도는 11로써 심플제로는 z0=1z_0 =1을 갖는다. 그러나 g(z)=(z−1)2=(z−1)(z−1)g(z)=(z-1)^2=(z-1)(z-1)라 할 때 z0=1z_0=1의 중복도는 22이므로 심플제로가 아니다.

Proof.

P3

Tn(x)T_n(x)의 극값의 위치와 그 값은
x^k=cos⁡(kπn),      with      Tn(x^k)=(−1)k,      for    each      k=0,1,⋯ ,n\hat{x}_k=\cos\bigg(\frac{k\pi}{n}\bigg),\;\;\; \mathbf{with}\;\;\; T_n(\hat{x}_k)=(-1)^{k},\;\;\; \mathbf{for \;\; each}\;\;\; k=0,1,\cdots,n
을 만족한다.

Proof.

P4

일계수 체비셰프 다항식(monic Chebyshev polynomials, 최고차항의 계수가 1인 다항식)은 아래와 같이 정의된다.
T~0(x)=1      and      T~n(x)=12n−1Tn(x),      for    each      n≥1.\tilde{T}_0(x)=1\;\;\;\mathbf{and}\;\;\;\tilde{T}_n(x)=\frac{1}{2^{n-1}}T_n(x),\;\;\;\mathbf{for\;\;each}\;\;\;n\ge1.
이를 체비셰프 점화식으로 표현하면
T~2(x)=xT~1(x)−12T~0(x)andT~n+1(x)=xT~n(x)−14T~n−1(x)for  each    n≥2.\begin{align*} \tilde{T}_2(x)&=x\tilde{T}_1(x)-\frac{1}{2}\tilde{T}_0(x) &\mathbf{and} \\ \tilde{T}_{n+1}(x)&=x\tilde{T}_n(x)-\frac{1}{4}\tilde{T}_{n-1}(x) &\mathbf{for\; each}\;\;n\ge2. \end{align*}
Proof. T~n(x)\tilde{T}_n(x)은 Tn(x)T_n(x)를 2n−12^{n-1}로 나눈식이므로 위 식이 성립하게 된다.

P5

T~n(x)\tilde{T}_n(x)의 모든 해는 아래 형태와 같고
xˉk=cos⁡(2k−12nπ),      for    each    k=1,2,⋯ ,n.\bar{x}_k=\cos\bigg(\frac{2k-1}{2n}\pi\bigg),\;\;\; \mathbf{for\;\;each}\;\;k=1,2,\cdots,n.
T~n(x)\tilde{T}_n(x)의 극점은 아래와 같다.
xˉk′=cos⁡(kπn),      with      T~n(xˉk′)=(−1)k2n−1,      for    each    n=0,1,2,⋯ ,n.\bar{x}^{\prime}_k=\cos\bigg(\frac{k\pi}{n}\bigg),\;\;\;\mathbf{with}\;\;\;\tilde{T}_n(\bar{x}^{\prime}_k)=\frac{(-1)^k}{2^{n-1}},\;\;\;\mathbf{for\;\;each}\;\;n=0,1,2,\cdots,n.
Proof. 이 또한 T~n(x)\tilde{T}_n(x)은 Tn(x)T_n(x)를 2n−12^{n-1}로 나눈식임을 이용하면 간단히 증명할 수 있다.

P 6

∏~n\tilde{\prod}_n을 모든 nn차 일계수 다항식의 집합이라고 하자.
다항식의 형식이 T~n(x)\tilde{T}_n(x)이고 n>1n>1일 때, 아래와 같은 성질을 갖는다.
12n−1=max⁡x∈[−1,1]∣T~n(x)∣≤max⁡x∈[−1,1]∣Pn(x)∣,      for    all      P(x)∈∏~n.\frac{1}{2^{n-1}}=\max_{x\in[-1,1]}{|\tilde{T}_n(x)|} \le \max_{x\in[-1,1]}{|P_n(x)|}, \;\;\;\mathbf{for\;\;all}\;\;\;P(x)\in\tilde{\prod}_n.
위 식은 Pn≡T~nP_n\equiv \tilde{T}_n일 때 만족한다.

Proof.

P 7

Tn(x)=2xTn−1(x)−Tn−2(x)    for    n≥2.T_n(x)=2xT_{n-1}(x)-T_{n-2}(x)\;\;\mathbf{for}\;\;n\ge2.
Proof. 본래 점화식에 n+1n+1을 대입하면 간단히 증명이 가능하다.

P 8

Tm(x)Tn(x)=12[Tm+n+Tm−n]    for    m>n.T_m(x)T_n(x)=\frac{1}{2}[T_{m+n}+T_{m-n}]\;\;\mathbf{for}\;\;m>n.
Proof. 삼각함수 공식 cos⁡(a)cos⁡(b)=12[cos⁡(a+b)+cos⁡(a−b)]\cos(a)\cos(b)=\frac{1}{2}[\cos(a+b)+\cos(a-b)]을 이용하여 증명한다.
Tm(x)⋅Tn(x)=cos⁡(marccos⁡(x))cos⁡(narccos⁡(x))=12[cos⁡((m+n)arccos⁡(x))+cos⁡((m−n)arccos⁡(x))]=12[Tm+n+Tm−n(x)].\begin{align*} T_m(x)\cdot T_n(x)&=\cos(m\arccos(x))\cos(n\arccos(x))\\ &=\frac{1}{2}[\cos((m+n)\arccos(x))+\cos((m-n)\arccos(x))] \\ &=\frac{1}{2}[T_{m+n}+T_{m-n}(x)]. \end{align*}

P 9

Tm(Tn(x))=Tmn(x).T_m(T_n(x))=T_{mn}(x).
Proof.
Tm(Tn(x))=cos⁡(marccos⁡(cos⁡(narccos⁡(x))))=cos⁡(mnarccos⁡(x))=Tmn(x).\begin{align*} T_m(T_n(x))&=\cos(m\arccos(\cos(n\arccos(x)))) \\ &=\cos(mn\arccos(x)) \\ &=T_{mn}(x). \end{align*}

P 10

Tn(x)=12[(x+x2−1)n+(x−x2−1)n].T_n(x)=\frac{1}{2}\bigg[(x+\sqrt{x^2-1})^n+(x-\sqrt{x^2-1})^n\bigg].

Proof.

P 11

∣x∣≥1|x|\ge 1인 모든 실수 xx에 대해 아래 수식이 성립하며,
12[(x+x2−1)n+(x−x2−1)n]=cosh⁡(ncosh⁡−1(x))\frac{1}{2}\bigg[(x+\sqrt{x^2-1})^n + (x-\sqrt{x^2-1})^n \bigg]=\cosh(n\cosh^{-1}(x))
따라서 모든 실수 xx에 대해
Tn(cosh⁡(x))=cosh⁡(nx)T_n(\cosh(x))=\cosh(nx)
가 성립한다.

Proof.

P 12

∣x∣>1|x|>1에 대해 Tn(x)≤(∣x∣+x2−1)nT_n(x)\le (|x|+\sqrt{x^2-1})^n가 성립한다.
Proof.
Tn(x)=12[(x+x2−1)n+(x−x2−1)n]≤12[2⋅(x+x2−1)n]=(x+x2−1)nT_n(x)=\frac{1}{2}\bigg[(x+\sqrt{x^2-1})^n + (x-\sqrt{x^2-1})^n \bigg] \le \frac{1}{2}\bigg[2 \cdot (x+\sqrt{x^2-1})^n \bigg]=(x+\sqrt{x^2-1})^n
따라서 Tn(x)≤(∣x∣+x2−1)nT_n(x)\le (|x|+\sqrt{x^2-1})^n가 성립한다.

P 13

nn이 홀수면
2nxn=∑k=0[n/2](nk)2Tn−2k(x)2^n x^n=\sum^{[n/2]}_{k=0}\begin{pmatrix}n\\k \end{pmatrix} 2 T_{n-2k} (x)
이고, nn이 짝수면 마지막 항은 2T02T_0가 아닌 T0T_0다.

Proof.

P 14

TnT_n과 Tn−1T_{n-1}은 공통근이 존재하지 않는다.
Proof. 귀류법을 활용한다. TnT_n과 Tn−1T_{n-1}이 공통근 x0x_0를 가진다고 하자. 그렇다면 Tn(x0)=0=Tn−1(x0)T_n(x_0)=0=T_{n-1}(x_0)가 성립한다. P7에 의해 Tn(x0)=0=2x0Tn−1(x0)−Tn−2(x)=−Tn−2(x)T_n(x_0)=0=2x_0T_{n-1}(x_0)-T_{n-2}(x)=-T_{n-2}(x)가 성립하므로 Tn−2(x0)T_{n-2}(x_0) 또한 00이 되어야 한다. 이를 반복하면 결국 k<nk < n인 모든 kk에 대해 kk가 00일때를 포함하여 Tk(x0)=0T_k(x_0)=0이 된다. 그러나 T0(x)=1T_0(x)=1이므로 이는 모순이다. 따라서 TnT_n과 Tn−1T_{n-1}은 공통근이 존재하지 않는다.

P 15

∣x∣≤1|x|\le1에 대해 ∣Tn′(x)∣≤n2|T^{\prime}_n(x)|\le n^2와 ∣Tn′(±1)∣=n2|T^{\prime}_n(\pm1)|=n^2이 성립한다.

Proof.