///
Search
📄

Integers and Equivalence Relation

본 문서에선 본격적으로 현대대수를 공부하기 전에 알아야하는 내용들을 담고있다. 정수와 집합에 대한 성질들을 다룬다.

Definition

a,b∈Z∗a,b\in\mathbb{Z}^{*} (:=Z−{0})(:= \mathbb{Z}-\{0\})에 대해서
•
gcd(a,b)=max⁡{d∈Z  :  d∣a,  d∣b}gcd(a,b)=\max\{d\in\mathbb{Z}\;:\;d|a, \;d|b\} (최대공약수)
•
lcm(a,b)=min⁡{n∈Z  :  a∣n,  b∣n}lcm(a,b)=\min\{n\in\mathbb{Z}\;:\;a|n,\;b|n\} (최소공배수)
•
gcd(a,b)=1⇒gcd(a,b)=1\Rightarrow aa와 bb는 서로소(relatively prime)*

example

•
lcm(−2,−3)=6lcm(-2,-3)=6
•
gcd(4,6)=2gcd(4,6)=2

Theorem (GCD is a linear combination)

00이 아닌 정수 aa와 bb에 대해 gcd(a,b)=as+btgcd(a,b)=as+bt를 만족하는 ss와 tt가 존재한다. 또한 gcd(a,b)gcd(a,b)는 as+btas+bt 형태로 만들 수 있는 수 중 가장 작은 양의정수다.

Corollary

만약 aa와 bb가 서로소(relatively prime)면 as+bt=1as+bt=1을 만족하는 ss와 tt가 존재한다.

example

•
gcd(4,15)=1→4⋅4+15⋅(−1)=1gcd(4,15)=1\rightarrow 4\cdot4 + 15\cdot(-1)=1
•
gcd(4,10)=2→4⋅(−2)+10⋅1=2gcd(4,10)=2 \rightarrow 4\cdot(-2)+10\cdot 1 =2

lemma (Euclid’s lemma)

만약 pp가 abab의 약수인 소수라면 aa 또는 bb가 pp로 나누어떨어진다.

example

•
5∣22⋅53→5∣535|2^2\cdot5^3\rightarrow 5|5^3
•
반례 6∣4⋅36|4\cdot3 그러나 6∤4,  6∤36\nmid4,\;6\nmid3 이다. (66은 소수가 아니기 때문)

Theorem (Fundamental Theorem of Arithmetic)

11보다 큰 모든 정수는 소수거나 소수들의 곱이다.
1.
만약 n∈Z>1n\in \mathbb{Z}_{>1}면, pip_i가 소수고 rj∈Z>0r_j \in \mathbb{Z}_{>0}일 때 (1≤i,j≤t)(1\le i,j \le t) n=p1r1⋯ptrtn=p_1^{r1}\cdots p^{r_t}_t가 성립한다.
2.
곱의 형태는 각 인자의 순서를 고려하지 않았을 때 유일(unique)하다.

example

36=22⋅32=2⋅2⋅3⋅3=2⋅3⋅3⋅2=⋯36=2^2\cdot 3^2=2\cdot 2 \cdot 3 \cdot 3=2\cdot 3 \cdot 3 \cdot 2 = \cdots

lemma

aa와 bb가 양의정수 일 때 ab=lcm(a,b)⋅gcd(a,b)ab=lcm(a,b)\cdot gcd(a,b)가 성립한다.

Proof.

Modular Arithmetic

a≡nb    (⇔a  mod  n=b  mod  n)a \underset n \equiv b\;\;(\Leftrightarrow a\;mod\;n=b\;mod\;n) :=n∣(a−b):= n|(a-b)

example

5≡325 \underset3 \equiv 2, −5≡31-5 \underset3 \equiv 1

Definition

집합 SS에 대해 동치관계(equivalent relation)* SS는 S의 원소를 순서쌍으로 가지고 아래 세 조건을 만족하는 집합 RR과 같다.
1.
(a,b)∈R,∀a∈S(a,b)\in R,^\forall a\in S : reflexive (a∼b)(a\sim b)
2.
(a,b)∈R(a,b)\in R이면 (b,a)∈R(b,a)\in R이다. : symmetric (a∼b⇒b∼a)(a\sim b \Rightarrow b \sim a)
3.
(a,b)∈R(a,b)\in R이고 (b,c)∈R(b,c)\in R이면 (a,c)∈R(a,c)\in R이다. : transitive (a∼b,b∼c⇒a∼c)(a\sim b, b\sim c \Rightarrow a \sim c)
정리하면 equivalent relation은 주어진 집합(SS)안에서 정해진 조건(∼\sim)으로 두 원소를 수행했을 때 reflexive, symmetric, transitive를 모두 만족하는 원소들의 집합(RR)을 말한다.

Definition

∼\sim가 집합 SS에서의 동치관계(equivalent relation)이고 a∈Sa\in S일 때, [a]={s∈S : a∼s} (⊂S)[a] = \{s\in S~:~a\sim s\}~(\subset S)은 aa를 포함하는 SS의 동치류(equivalence class)*이다.

example

S={ triangles in R2}, a,b,c∈SS=\{~triangles~in~\mathbb{R}^2\},~a,b,c \in S
a∼b⇔△∼△′a\sim b \Leftrightarrow \triangle \sim \triangle^{\prime} (similar; 닮음)
1.
△∼△\triangle \sim \triangle
2.
△∼△′⇒△′∼△\triangle \sim \triangle^{\prime}\Rightarrow \triangle^{\prime} \sim \triangle
3.
△∼△′,△′∼△′′⇒△∼△′′\triangle \sim \triangle^{\prime},\triangle^{\prime}\sim\triangle^{\prime\prime}\Rightarrow \triangle\sim\triangle^{\prime\prime}

example

S=R[x]S=\mathbb{R}[x] (R\mathbb{R}의 원소를 xx의 계수로 가지는 다항식), f,g∈S,~f,g\in S
f∼g⇔f′=g′f\sim g\Leftrightarrow f^{\prime}=g^{\prime}
1.
f∼f (∵f′=f′)f\sim f~(\because f^{\prime}=f^{\prime})
2, 3번 조건은 당연(trivial)하다.

example

S=ZS=\mathbb{Z}
a∼b⇔a≡nba\sim b \Leftrightarrow a \underset n \equiv b
ex) n=3→1∼4, 0∼3n=3 \rightarrow 1 \sim 4,~0\sim 3. [5]={⋯ ,−4,−1,2,5,8,⋯ }[5]=\{\cdots,-4,-1,2,5,8,\cdots\}
1.
a≡na⇔n∣(a−a)a\underset n \equiv a \Leftrightarrow n | (a-a)
2.
a≡nb⇔n∣(a−b)⇔n∣(b−a)⇔b≡naa \underset n \equiv b \Leftrightarrow n | (a-b) \Leftrightarrow n | (b-a) \Leftrightarrow b \underset n \equiv a

example

S={(a,b)∈Z2 : b≠0}S=\{(a,b)\in\mathbb{Z}^2~:~b\neq0\}
ab∼cd→(a,b)∼(c,d)⇔ad=bc→ab=cd\frac{a}{b}\sim \frac{c}{d} \rightarrow (a,b)\sim(c,d) \Leftrightarrow ad=bc \rightarrow \frac{a}{b}=\frac{c}{d}
1.
(a,b)∼(a,b)   (∵ab=ab)(a,b)\sim(a,b)~~~(\because ab=ab)
2.
(a,b)∼(c,d)⇒(c,d)∼(a,b)   (∵ad=bc⇔cb=ad)(a,b)\sim(c,d)\Rightarrow (c,d)\sim(a,b)~~~(\because ad=bc \Leftrightarrow cb=ad)
(1,2)≠(2,4)(1,2)\neq (2,4)이지만 (1,2)∼(2,4)(1,2)\sim (2,4)는 성립함.
∴[(1,2)]={(1,2),(2,4),⋯ }\therefore [(1,2)]=\{(1,2),(2,4),\cdots \}

Definition

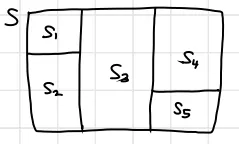
SS에 대한 파티션(partition)은 합집합(union)이 SS가 되는 공집합(non empty)이 아니고 서로소(disjoint)인 SS의 부분집합(subset)들의 모음(collection)이다.
파티션(partition)은 각각 겹치지 않지만 모두 합치면 SS가 되는 컬렉션을 의미한다.

example

•
Z=2Z+(2Z+1)\mathbb{Z}=2\mathbb{Z} + (2\mathbb{Z}+1) 2Z2\mathbb{Z}는 짝수, (2Z+1)(2\mathbb{Z}+1)는 홀수
•
반례 Z=Z≥0+Z≤0\mathbb{Z}=\mathbb{Z}_{\ge 0} + \mathbb{Z}_{\le 0}는 partition이 아니다. ({0}\{0\}이 겹치므로 서로소가 아님)
•
Z=Z++{0}+Z−\mathbb{Z}=\mathbb{Z}^{+}+\{0\}+\mathbb{Z}^{-}

Theorem (Equivalence Class Partition)

공집합이 아닌 집합 SS에 대해
1.
SS의 동치관계(equivalence relation)에 대한 동치류(equivalence class)는 SS의 파티션(partition)이 된다.
2.
SS의 임의의 파티션(partition) PP에 대해 동치류(equivalence class)들이 PP의 원소가 되는 SS에 대한 동치관계(equivalence relation)가 존재한다.

Proof.

Definition

S/∼  :=  {[a]:a∈S}S/\sim ~~ :=~~\{[a]:a\in S\}를 quotient set*이라 한다.
즉, 동치류(equivalence class)들을 원소로 하는 집합을 말한다.

Definition

집합 AA의 원소 aa가 집합 BB의 원소 bb 하나에 할당이 되는 규칙(rule)을 집합 AA에서 집합 BB로 가는 함수(function 또는 mapping)*라 한다.

Theorem (Properties of Functions)

함수 α:A→B, β:B→C, γ:C→D\alpha:A\rightarrow B,~\beta:B\rightarrow C,~ \gamma:C\rightarrow D가 주어졌을 때, 아래 네가지 성질(properties)을 만족한다.
1.
γ⊙(β⊙α)=(γ⊙β)⊙α\gamma \odot (\beta \odot \alpha)= (\gamma \odot \beta) \odot \alpha : 결합법칩(associativity)
2.
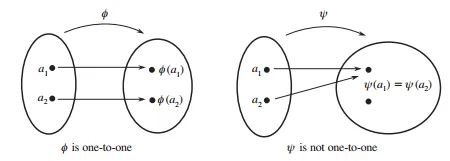
α,β\alpha,\beta가 일대일 함수(1-1)면 β⊙α\beta \odot \alpha 또한 일대일 함수다.
3.
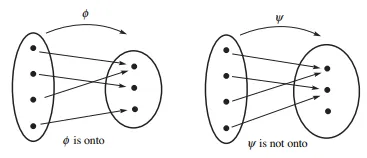
α,β\alpha,\beta가 대응함수(onto)면 β⊙α\beta \odot \alpha 또한 대응함수다.
4.
α\alpha가 일대일 대응함수(1-1 + onto)면 (α−1⊙α)(a)=a(\alpha^{-1} \odot \alpha)(a)=a를 만족하는 α−1:B→A\alpha^{-1}:B\rightarrow A가 존재한다.
[참고]
일대일 함수
대응함수