///
Search
📄

Chapter 1.2: Change of Coordinates

본 챕터에선 좌표변환(change of coordinate)에 대해 다룬다. 특정 공간을 좀 더 쉽게 이해하고 연산하거나 새로운 성질을 찾기 유용하게 좌표계(coordinate)를 변경할 수 있다. 이러한 과정을 진행하기 위해서 먼저 아핀공간(affine space)에 대해 소개하고 이를 통한 좌표변환(change of coordinate)을 여러 예제를 통해 다뤄본다.

Definition

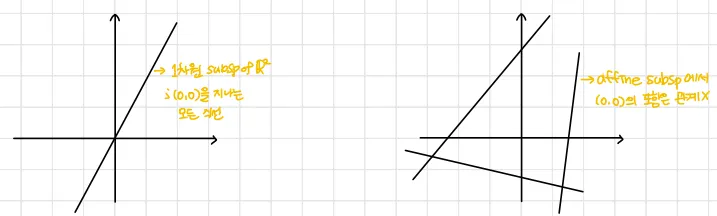
집합(set)의 관점에서 서로 같은 집합 AA와 VV에 대해 (A,l:V×A→A)(v,a)↦v⃗+a(A,l:\underset{(v,a)\mapsto \vec{v}+a}{V\times A\rightarrow A)}로 정의되고 아래 세가지 성질을 만족하는 공간을 아핀공간(Affine space)이라 한다.
1.
(좌측연산 항등원; left identity) ∀a∈A,0⃗+a=a^{\forall}a\in A, \vec{0}+a=a
2.
(결합법칙; associativity) ∀v,w∈V,∀a∈A,v⃗+(w⃗+a)=(v⃗+w⃗)+a^{\forall}v,w \in V, ^{\forall}a\in A, \vec{v}+(\vec{w}+a)=(\vec{v}+\vec{w})+a
3.
(유일성; uniqueness) ∀a∈A,V→Av⃗↦v⃗+a^{\forall}a \in A, \underset{\vec{v}\mapsto \vec{v}+a}{V\rightarrow A}는 일대일대응(bijective)이다.
벡터 공간(vector space)와 유사한 점이 많으나 벡터공간(vector space)과 달리 아핀공간(affine space)는 부분공간(subspace)를 잡을 때 영벡터에 대해 신경쓰지 않아도 된다.

Example

•
V,WV,W가 벡터 스페이스(vector space)일 때 선형 변환(linear transformation)은 f:V⟶Wv⃗⟼M⋅v⃗      ;w⃗=Mv⃗f:\underset{\vec{v}\longmapsto \mathbf{M}\cdot \vec{v}}{V\longrightarrow W}\;\;\;;\vec{w}=\mathbf{M}\vec{v}
•
X,YX,Y가 아핀공간(affine space)일 때 아핀 변환(affine transformation)은 f:X⟶Yf:X\longrightarrow Y에 대해 M:X⟶YdetM≠0\underset{det\mathbf{M}\neq 0}{\mathbf{M}:X\longrightarrow Y}이 선형변환(linear transformation)일 때 f(x)=Mx+b    (b∈Y)f(x)=\mathbf{M}x+b\;\;(b\in Y)이다. 여기서 M\mathbf{M}은 회전(rotation)과 스케일(scale)이고 bb는 평행이동(translation)이다. 영벡터에 대해 신경쓰지 않아도 되기 때문에 bb가 00이 아니어도 된다.

Exercise 1.2.1

(degree 1) R2\mathbb{R}^2에서 ax+by+c=0ax+by+c=0은 M\mathbf{M}과 bb를 잘 잡아서 y=0y=0으로 만들어줄 수 있다 (예. a=c=0,  b=1a=c=0,\;b=1).
(degree 2) P(x,y)=ax2+bxy+cy2+dx+ey+hP(x,y)=ax^2+bxy+cy^2+dx+ey+h

Definition

R2\mathbb{R}^2에서 아핀 좌표 변환(Affine change of coordinates)은 아래와 같다.
(uv)=(abcd)(xy)+(ef),          {a,b,c,d,e,f∈Rad−bc≠0\bigg(\begin{matrix}u\\v\end{matrix}\bigg)=\bigg(\begin{matrix}a&b\\c&d \end{matrix}\bigg)\bigg(\begin{matrix}x \\ y \end{matrix}\bigg)+\bigg(\begin{matrix}e\\f\end{matrix}\bigg) ,\;\;\;\;\;\begin{cases}a,b,c,d,e,f \in \mathbb{R} \\ ad-bc\neq 0\end{cases}
u=ax+by+eu=ax+by+e v=cx+dy+fv=cx+dy+f 에 대해 (0,0)(0,0)을 변환해도 여전히 (u,v)(u,v)가 (0,0)(0,0)이라면 e=f=0e=f=0이 된다.

Exercise 1.2.2

{u=ax+by+ev=cx+dy+f\begin{cases} u=ax+by+e \\ v=cx+dy+f \end{cases}에 대해 좌표 역변환(inverse change of coordinate)은 {x=(1ad−bc)(du−bv)−(1ad−bc)(de−bf)y=(1ad−bc)(−cu+dv)−(1ad−bc)(−ce+df)\begin{cases} x=\big(\frac{1}{ad-bc}\big)(du-bv)-\big(\frac{1}{ad-bc}\big)(de-bf)\\ y=\big(\frac{1}{ad-bc}\big)(-cu+dv)-\big(\frac{1}{ad-bc}\big)(-ce+df) \end{cases}임을 보여라.

Proof.

Exercise 1.2.3

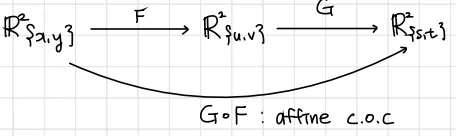
아핀 좌표변환(affine change of coordinate)은 합성도 가능하다. 즉 아핀(affine)변환은 합성을 해도 아핀(affine)변환이다.

Exercise 1.2.4(4), 1.2.5(5), 1.2.6(5)

아래 식의 실수(real) 아핀 좌표변환(affine change of coordinate)를 찾아라
1.
ellipse: V(13x2−10xy+13y2−1)→V(4u2+9v2−1)V(13x^2-10xy+13y^2-1)\rightarrow V(4u^2+9v^2-1)
2.
hyperbola: V(8xy−1)→V(2u2−2v2−1)V(8xy-1)\rightarrow V(2u^2-2v^2-1)
3.
parabola: V(4x2+4xy+y2−y+1)→V(4u2+v)V(4x^2+4xy+y^2-y+1)\rightarrow V(4u^2+v)

Solution.

Exercise 1.2.8

아래 실수 아핀 변환(real affine transformation)이 xy평면(xy-plane)에서 타원 C\mathcal{C}에 적용됬을 때 (1)Au2+Cv2+Du+Ev+H=0Au^2+Cv^2+Du+Ev+H=0으로 표현됨을 보여라.
x=cau+vy=u−acvx=\sqrt{\frac{c}{a}u}+v\\ y=u-\sqrt{\frac{a}{c}v}
또한 (2)AA와 CC를 a,b,ca,b,c항으로 표현하고 (3)b2−4ac>0b^2-4ac>0라면 A≠0A\neq 0이고 C≠0C\neq 0임을 보여라.

Solution

Exercise 1.2.9

Au2+Cv2+Du+Ev+H=A(u−R)2+C(v−S)2−TAu^2+Cv^2+Du+Ev+H=A(u-R)^2+C(v-S)^2-T에 대해 R,S,TR,S,T를 A,C,D,E,HA,C,D,E,H로 표현하라.

Solution

Exercise 1.2.10

아래와 같이 포물선(hyperbola) V(x,y)V(x,y)를 포물선(hyperbola) v(u,v)v(u,v)로 보내는 실수 아핀 좌표변환(real affine change of coordinate) FF를 찾아라.
V(A(x−R)2+C(y−S)2−T)⟶V(u2+v2−1)V(A(x-R)^2+C(y-S)^2-T)\longrightarrow V(u^2+v^2-1)

Solution

Exercise 1.2.20

다른 클래스는 서로 변환이 불가능함을 확인한다. 이를 위해 타원(ellipse)과 쌍곡선(hyperbola)에 대해 확인한다. 귀류법을 활용하기 위해 두 이차곡선이 변환이 가능하다고 가정한다.
C=V(X2+Y2−1)C=V(U2−V2−1)(uv)=(abcd)(XY)+(ef)⟶{U=aX+bY+eV=cX+dY+fC=V(X^2+Y^2-1)\\ C=V(U^2-V^2-1)\\ \begin{pmatrix}u \\ v\end{pmatrix} = \begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}X\\Y\end{pmatrix}+\begin{pmatrix}e\\f\end{pmatrix} \longrightarrow \begin{cases}U=aX+bY+e\\ V=cX+dY+f \end{cases}
X2+Y2=U2−V2X^2+Y^2=U^2-V^2이고 X2+Y2=(aX+bY+e)2−(cX+dY+f)2X^2+Y^2=(aX+bY+e)^2-(cX+dY+f)^2이므로 X2X^2의 계수는 a2−c2=1⇒(a+c)(a−c)=1⇒∣a∣≠∣c∣a^2-c^2=1 \Rightarrow (a+c)(a-c)=1 \Rightarrow |a|\neq |c| XX의 계수는 2ae−2cf=0⇒ae=cf2ae-2cf=0 \Rightarrow ae=cf 상수항은 e2−f2=0⇒(e+f)(e−f)=0⇒∣e∣=∣f∣e^2-f^2=0\Rightarrow (e+f)(e-f)=0 \Rightarrow |e|=|f|이다. 이 때 ae=cfae=cf라 했으므로 ∣a∣=∣c∣|a|=|c|여야 하는데 이는 위 ∣a∣≠∣c∣|a|\neq |c|와 모순되므로 두 이차곡선은 변환이 불가능하다.

Definition

C=V(F),C′=V(F′)⊂R2C=V(F),C^{\prime}=V(F^{\prime})\subset \mathbb{R}^2에서 A:R2→R2A:\mathbb{R}^2\rightarrow \mathbb{R}^2에 대해 F′=AFF^{\prime}=AF인 실수 아핀 좌표변환(real affine change of coordinate)이 존재한다면, CC와 C′C^{\prime}을 동등하다(equivalent)고 한다.