본 문서는 대수기하에 대한 내용을 다루며 특히, 비 유클리드 공간에서 평면대수공간에 대한 것을 다룹니다.
유클리드 공간
1.
두 점을 잇는 직선은 유일하다
2.
두 점을 잇는 선분은 무한대로 늘릴 수 있다
3.
임의의 한 점과 임의의 길이를 반지름으로 하는 원을 그릴 수 있다.
4.
직각은 모두 같다
5.
평행선 공리: 두 직선이 한 직선과 만날 때 같은 쪽에 있는 내각의 합이 보다 작으면 두 직선을 연장할 때 반드시 내각이 보다 작은 쪽에서 반드시 만난다.
이 중 5번째 공리, 평행선 공리가 성립하지 않는 공간을 비 유클리드 공간이라고 합니다.
들어가기 전에
대수기하(Algebraic Geometry)는 연립다항식들의 공통근으로 이뤄진 공간을 연구하는 학문이다. 즉 1차 다항식으로 직선 또는 평면을, 2차 다항식으로 타원이나 포물선, 쌍곡선 등을 분석하는 등 대수학을 이용하여 기하를 연구하는 학문을 말한다.
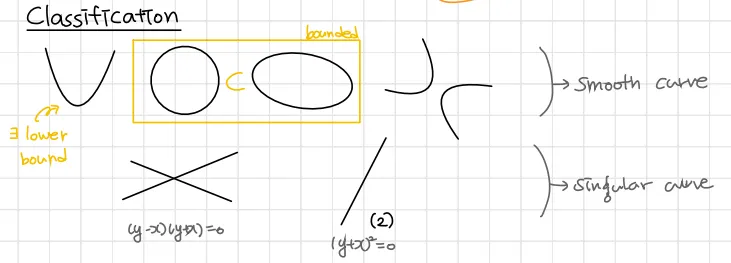
차원이 이라면 유한개의 점을 의미하고 차원이 이라면 곡선(curve)을 의미하며 곡선(curve)엔 직선(line), 타원곡선(elliptic curve) 등이 있다. 타원곡선(elliptic curve)는 아래 그림과 같이 분류된다.
대수기하학에서 타원곡선(elliptic curve)을 간단히 설명하면 형태의 방정식으로 정의되는 대수곡선을 말한다. 첨점이나 교차점 등의 특이점이 없다는 특징이 있으며 자세한건 이후 챕터에서 다루게 될 것이다.
대수기하는 다항식의 공통근 연구를 목적으로 여러 대수학적 방법론과 기하의 언어를 합친 학문이며 대수학과 기하위상수학이 만나는 분야가 된다.
목차
참조
본 문서는 [장은진 선생님의 수학자료]를 정리한 내용으로 대부분의 내용을 해당문서에서 참조합니다. 나머지 참조내용은 각 문서의 하단에 적었습니다.