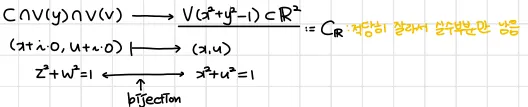Search
📄

Chapter 1.3: Conics over the Complex Numbers

💡
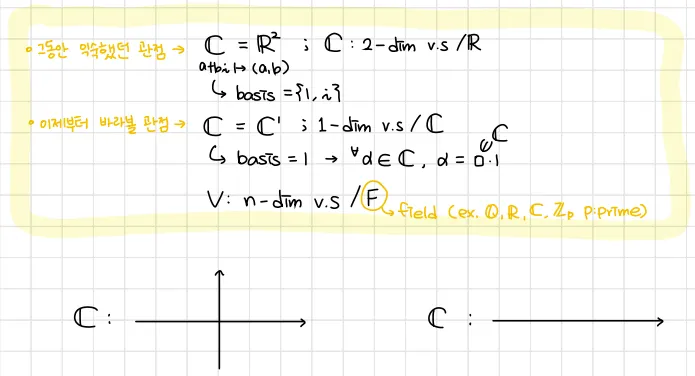
실수공간과 달리 복소공간에서의 곡선(conic)에 대해선 모든 문제가 완전히 해결되었다. 그 동안 익숙했던 관점은 복소수를 a+bia+bi꼴로써 실수와 허수를 분리하였다. 즉, 이차원의 실수공간으로 바라보는것이었다. 지금부턴 일차원의 복소수 자체를 다루며 본 챕터에선 복소공간에서의 이차곡선에 대해 살펴본다.

Theorem (The Fundamental Theorem of Algebra)

F(x)∈C[x]:={a0+a1x+⋯+anxn:ai∈C,  n∈Z≥0}F(x)\in\mathbb{C}[x]:=\{a_0+a_1x+\cdots + a_nx^n:a_i\in\mathbb{C},\;n\in\mathbb{Z}_{\geq0}\}에서 degF(x)=ndegF(x)=n일 때 F(x)F(x)는 반드시 nn개의 복소해를 갖는다.

Example

•
x2+1=0x^2+1=0은 실수해를 갖지 않는다.
•
x2+1=0x^2+1=0은 2개의 복소해를 갖는다. (C:±i\mathbb{C}:\pm i)

Exercise 1.3.1

C(F):={(x,y)∈F2:x2+y2+1=0}C(F):=\{(x,y)\in F^2:x^2+y^2+1=0\}에 대해
•
C(R)=∅;C(\mathbb{R})=\empty; (0≤x2+y2=−1 0 \leq x^2+y^2 =-1이므로)
•
C(C)≠∅;C(\mathbb{C})\neq \empty; x∈Cx\in\mathbb{C}, y2=−x2−1⇒y=±−x2−1y^2=-x^2-1 \Rightarrow y=\pm \sqrt{-x^2-1}이므로 x≠±ix\neq \pm i면 yy는 두 개의 해를 갖는다. x=±ix=\pm i면 yy는 한 개의 해를 갖는다.(중근)

Exercise 1.3.2

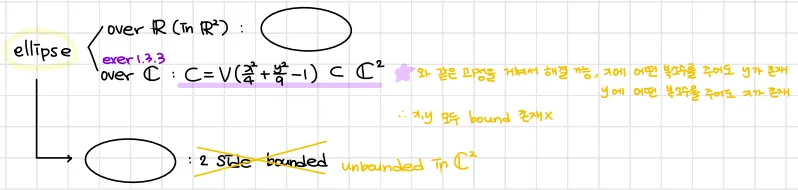
타원을 복소공간에서 다뤘을 때 어떻게 되는지 확인하기 위해 아래 문제를 풀어보자.
(a≠0)P(x,y)=ax2+bxy+cy2+dx+ey+f(a\neq0)P(x,y)=ax^2+bxy+cy^2+dx+ey+f에서 어떤 y∈Cy\in\mathbb{C}에 대해 P(x,y)=0P(x,y)=0인 x∈Cx\in\mathbb{C}가 적어도 1개, 최대 2개 존재함을 보여라.

Proof.

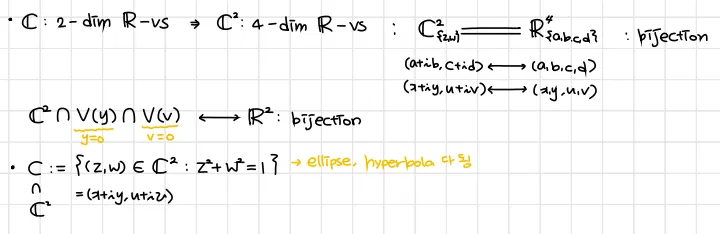
타원(ellipse)는 실수에선 근이 없을 수 도 있는것과 다르게 복소수에선 항상 근이 존재한다. 이를 통해 아래와 같은 사실을 알아낼 수 있다.
⚠️ 실수 공간에서 타원은 경계(bound)가 존재한다. 즉, 어떤 xx 또는 yy는 이에 해당하는 yy와 xx가 존재하지 않을 수 있다. 그러나 복소공간에선 항상 근이 존재하므로 경계가 없다(unbounded).

Exercise 1.3.4

쌍곡선(hyperbola)을 복소공간에서 다뤘을 때 어떻게 되는지 확인하기 위해 아래 문제를 풀어보자.
C=V(x2−y2−1)⊂C2C=V(x^2-y^2-1)\subset \mathbb{C}^2에서 (−1,0)(-1,0)에서 (1,0)(1,0)으로 가는 연속경로(continuous path)가 존재함을 보여라

Proof.

Exercise 1.3.5

V(X2+Y2−1)⊂C{X,Y}2V(U2−V2−1)⊂C{U,V}2{U=XV=iY⟶(UV)=(100i)(XY)\begin{align*} &V(X^2+Y^2-1)\subset \mathbb{C}^2_{\{X,Y\}} \\ &V(U^2-V^2-1) \subset \mathbb{C}^2_{\{U,V\}} \\ &\begin{cases} U=X \\ V=iY \end{cases} \longrightarrow \begin{pmatrix}U\\V\end{pmatrix}=\begin{pmatrix}1&0\\0&i\end{pmatrix}\begin{pmatrix}X\\Y\end{pmatrix} \end{align*}

Definition

복소공간 C2\mathbb{C}^2에서 아래와 같은 조건을 만족할 때 이를 복소 아핀 좌표변환(complex affine change of coordinate)이라 한다.
F:C{x,y}2⟶C{u,v}2F:\mathbb{C}^2_{\{x,y\}}\longrightarrow \mathbb{C}^2_{\{u,v\}}가 (uv)=(abcd)(xy)+(ef)⋯(∗)\begin{pmatrix}u\\v\end{pmatrix}= \begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}+\begin{pmatrix}e\\f\end{pmatrix}\cdots(*)의 형식이고 (abcd)∈GL2(C),    e,f∈C\begin{pmatrix}a&b\\c&d\end{pmatrix}\in GL_2(\mathbb{C}),\;\;e,f\in\mathbb{C}이다.

Exercise 1.3.7

역변환(inverse transform) F−1:C{u,v}2⟶C{x,y}2F^{-1}:\mathbb{C}^2_{\{u,v\}}\longrightarrow\mathbb{C}^2_{\{x,y\}}을 구하여라

Definition

C=V(f),  C′=V(F′)⊂C2C=V(f),\;C^{\prime}=V(F^{\prime})\subset \mathbb{C}^2일 때 C≅C′:C\cong C^{\prime}: 복소공간 C\mathbb{C}에서 동일하다(equivalent over C\mathbb{C}) ⇔\Leftrightarrow 좌표(coordinate) FF의 어떤 복소 아핀 좌표변환(complex affine change of coordinate)이 f′=F(f)f^{\prime}=F(f)이다.

Exercise 1.3.7

모든 타원(ellipse)와 쌍곡선(hyperbola)는 복소공간 C\mathbb{C}에서(over) 복소 아핀 좌표변환(complex affine change of coordinate)하에 동일하다.

Proof.

⚠️ 복소공간에서(over complex space) 타원(ellipse)와 쌍곡선(hyperbola)는 서로 동일 클래스(equivalent class)다. 그러나! 포물선과는 동일관계(equivalent relation)이 존재하지 않는다.

Exercise 1.3.8

타원(ellipse)와 포물선(parabola)이 동일관계(equivalent relation)이 존재하지 않음을 확인한다.
C=V(x2+y2−1)≆CV(u2−v)=C′C=V(x^2+y^2-1)\underset{\mathbb{C}}{\ncong} V(u^2-v)=C^{\prime}을 보여라

Proof.

⚠️ 본 과목에서 바라보는 기하 배경은 R2→C2→PC2\mathbb{R^2\rightarrow C^2\rightarrow P_C^2}이고 R2→C2\mathbb{R^2\rightarrow C^2}를 유클리드 기하, C2→PC2\mathbb{C^2\rightarrow P_C^2}를 비유클리드 기하라 한다.

Exercise 1.3.9

CRC_{\mathbb{R}}를 복소 이차곡선(complex conic) CC에서의 리얼 슬라이스(real slice)라 한다.

Exercise 1.3.10