///
Search
📄

Chapter 1.4: The Complex Projective Plane

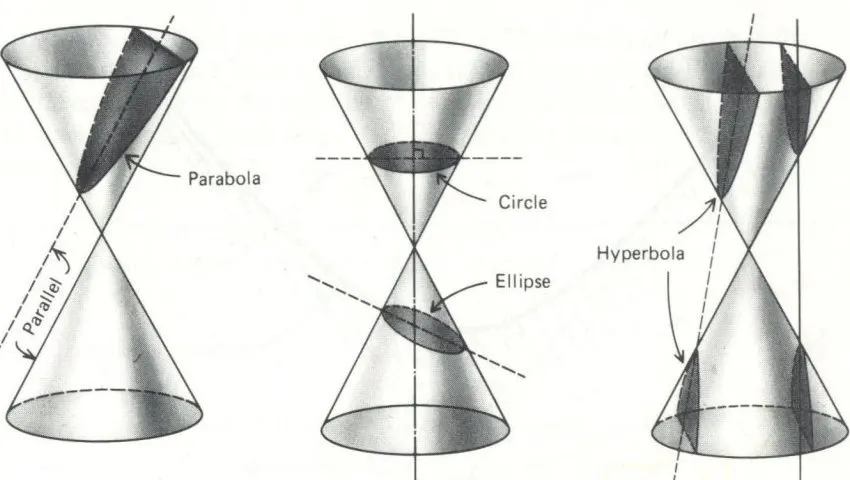
“평행한 두 직선은 만나지 않는다”가 유클리드 기하(euclidean geometry)였다면 비유클리드 기하인 사영기하에선 “모든 두 직선은 반드시 만난다”에 대한 가정을 기반으로 한다.
•
Akn:=kn    (k=R,C,Q,Fp,    p:prime)\mathbb{A}^n_k:=k^n\;\;(k=\mathbb{R,C,Q,F_p},\;\;p:prime) nn차원 아핀공간(affine space)
•
C⊂Ak2:C\subset \mathbb{A}^2_k: 이차식이며 k=R,C  (R2,C2)k=\mathbb{R,C\;(R^2,C^2)}으로 둘 수 있다.
•
공간이 Q,Fp\mathbb{Q,F_p}일 경우 아래와 같이 정리된다.
◦
C={(x,y)∈Q2:x2+y2=1}⊂Q2C=\{(x,y)\in\mathbb{Q}^2:x^2+y^2=1\}\subset \mathbb{Q}^2
◦
X={(x,y,z)∈Q3:x2+y2=z2}⊂Q3X=\{(x,y,z)\in \mathbb{Q}^3:x^2+y^2=z^2\} \subset \mathbb{Q}^3. 피타고라스 삼조(pythagorean triples). x2+y2=z2x^2+y^2=z^2을 만족하는 3개의 정수 집합 (x,y,z)(x,y,z)에 대해 gcd(x,y,z)=1gcd(x,y,z)=1을 만족하면 프리미티브(primitive)라고 한다.
◦
X(R)={(x,y,z)∈R3:x2+y2=z2}⊂R3X(\mathbb{R})=\{(x,y,z)\in\mathbb{R}^3:x^2+y^2=z^2\}\subset \mathbb{R}^3. 이차 콘(quadratic cone).
•
C→\mathbb{C}\rightarrow대수적으로 닫힌 필드(algebraically closed field). k=kˉk=\bar{k}
•
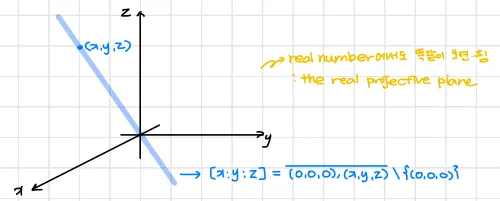
PC2\mathbb{P}^2_{\mathbb{C}}: 복소 사영 평면(complex projective plane). 복소(complex)는 C\mathbb{C}, 사영(projective)는 P\mathbb{P}, 평면(plane)은 22에 해당한다.

Definition

C3\{(0,0,0)}\mathbb{C}^3\backslash\{(0,0,0)\}에서 (x,y,z)∼(u,v,w)(x,y,z)\sim(u,v,w) ⟺def\overset{def}{\Longleftrightarrow} (x,y,z)=(λu,λv,λw)(x,y,z)=(\lambda u,\lambda v, \lambda w)을 만족하는 λ∈C\{0}\lambda\in \mathbb{C}\backslash \{0\}가 존재한다.

example

•
(1,2,3)∼(4,8,12);  λ=4(1,2,3)\sim(4,8,12);\;\lambda=4
•
(2,1+i,3i)∼(2−2i,2,3+3i);  λ=1−i(2,1+i,3i)\sim(2-2i,2,3+3i);\;\lambda=1-i

Exercise 1.4.2 ~ is an equivalent relation

Proof.

Exercise 1.4.3

(x1,y1,z1)∼(x2,y2,z2)(x_1,y_1,z_1)\sim(x_2,y_2,z_2)일 때 만약 x1=x2≠0x_1=x_2\neq 0이면 y1=y2y_1=y_2이고 z1=z2z_1=z_2이다.

Exercise 1.4.4

(x1,y1,z1)∼(x2,y2,z2)(x_1,y_1,z_1)\sim(x_2,y_2,z_2)일 때 z1≠0z_1\neq0이고 z2≠0z_2\neq 0이다. ⇒\Rightarrow(x1,y1,z1)∼(x1z1,y1z1,1)(x_1,y_1,z_1)\sim(\frac{x_1}{z_1},\frac{y_1}{z_1},1)이고 (x2,y2,z2)∼(x2z2,y2z2,1)(x_2,y_2,z_2)\sim(\frac{x^2}{z_2},\frac{y_2}{z_2},1)이다. ⇒\Rightarrow(x1z1,y1z1,1)∼(x1,y1,z1)∼(x2,y2,z2)∼(x2z2,y2z2,1)(\frac{x_1}{z_1},\frac{y_1}{z_1},1)\sim(x_1,y_1,z_1)\sim(x_2,y_2,z_2)\sim (\frac{x_2}{z_2},\frac{y_2}{z_2},1)이다.
동치 클래스(equivalent class) : (x:y:z):=[(x,y,z)]={(u,v,w)∈C3\{(0,0,0)}:(u,v,w)∼(x,y,z)}(x:y:z):=[(x,y,z)]=\{(u,v,w)\in\mathbb{C}^3\backslash\{(0,0,0)\}:(u,v,w)\sim(x,y,z)\}

Exercise 1.4.5

•
(0:0:1)={(0,0,t):t∈C∗}(0:0:1)=\{(0,0,t):t\in\mathbb{C}^{*}\}
•
(1:2:3)={(t,2t,3t):t∈C∗}(1:2:3)=\{(t,2t,3t):t\in\mathbb{C}^*\}
•
(1:2:3)=(2:4:6)      and      (1,2,3)∼(2,4,6)(1:2:3)=(2:4:6)\;\;\;and\;\;\;(1,2,3)\sim(2,4,6)
C∗\mathbb{C}^{*}는 공간 C\mathbb{C}에서 {0}\{0\}이 빠진 공간을 의미한다.
==는 같다(same)의 의미이고 ∼\sim은 관계가 있다(equivalent)의 의미이다.

Definition

PC2:=C3\{(0,0,0)}/∼=\mathbb{P}^2_{\mathbb{C}}:=\mathbb{C}^3\backslash\{(0,0,0)\}/_\sim={\{(0,0,0)(0,0,0)을 지나는 C3\mathbb{C}^3 위의 직선(line)들}\}을 복소사영평면(complex projective plane)이라고 한다.
무한대 선(line at infinity) : {(x:y:z)∈PC2:z=0}↔(x,y,z)∈R3\z\{(x:y:z)\in\mathbb{P}^2_\mathbb{C}:z=0\} \leftrightarrow (x,y,z)\in \mathbb{R}^3\backslash z 이차원에서 하나의 원소를 뺐기 때문에 직선이 된다.

Exercise 1.4.8

만약 c≠0c\neq 0이라면 L:(x=λa,y=λb,z=λc)L:(x=\lambda a, y=\lambda b, z=\lambda c)
P={(x,y,z):z=1}⇒∣L∩P∣=1P=\{(x,y,z):z=1\}\Rightarrow |L\cap P|=1
L∩P={(ac:bc:1)}L\cap P=\{(\frac{a}{c}:\frac{b}{c}:1)\}
L⟷bij(a:b:c)=(ac:bc:1)∈P∩LL\overset{bij}{\longleftrightarrow} (a:b:c)=(\frac{a}{c}:\frac{b}{c}:1) \in P\cap L : LL을 결정하는것은 a,b,ca,b,c로 (a:b:c)(a:b:c)는 유일(unique)하게 LL을 정의한다. 즉, 유일성(unique)와 존재성(exist)를 모두 만족하고 일대일 대응(bijective)를 만족한다.
위 내용과 무한대 선(infinity line)을 기반으로 PC2\mathbb{P}^2_\mathbb{C}을 다시 살펴보자.
PC2={(x:y:z)∈PC2:z≠0}  ∪˙  {(x:y:z)∈PC2:z=0}\mathbb{P}^2_\mathbb{C}=\{(x:y:z)\in \mathbb{P}^2_\mathbb{C}:z\neq0\} \;\dot{\cup}\; \{(x:y:z)\in\mathbb{P}^2_\mathbb{C}:z=0\}
∪˙\dot{\cup}는
{(x:y:z)∈PC2:z≠0}={(xz:yz:1)∈PC2}={(x′:y′:1)∈PC2=C{x′,y′}2\{(x:y:z)\in \mathbb{P}^2_\mathbb{C}:z\neq0\}\\ = \{(\frac{x}{z}:\frac{y}{z}:1)\in\mathbb{P}^2_\mathbb{C}\}\\=\{(x^\prime:y^\prime:1)\in \mathbb{P}^2_\mathbb{C} = \mathbb{C}^2_{\{x^\prime,y^\prime\}}
{(x:y:z)∈PC2:z=0}={(x:y:0)∈PC2=L∞\{(x:y:z)\in\mathbb{P}^2_\mathbb{C}:z=0\}\\ =\{(x:y:0)\in \mathbb{P}^2_\mathbb{C} \\ =L_\infty (무한대 선(line at infinity))
정리하면 PC2=C{x′,y′}2∪L∞\mathbb{P}^2_\mathbb{C}=\mathbb{C}^2_{\{x^\prime,y^\prime\}} \cup L_\infty가 된다.

Exercise

ϕ:C2⟶{(x:y:z)∈PC2:z≠0}=(z≠0)\phi:\mathbb{C}^2\longrightarrow \{(x:y:z)\in\mathbb{P}^2_\mathbb{C}:z\neq0\}=(z\neq0) (x,y)⟼(x:y:1)(x,y)\longmapsto (x:y:1)
일 때 ϕ\phi는 일대일 대응(bijective)이다.

Proof.

Exercise

ϕ\phi의 역함수 ϕ−1\phi^{-1}에 대해 살펴본다. 우선 ϕ−1\phi^{-1}는 아래와 같이 표현된다.
ϕ−1:(z≠0)⟶C2(x:y:z)⟼(xz,yz)\underset{(x:y:z)\longmapsto (\frac{x}{z},\frac{y}{z})}{\phi^{-1}:(z\neq0)\longrightarrow \mathbb{C}^2}
역원이란 연산해서 항등원을 만드는 것을 말하고 역함수는 합성연산을 했을 때 항등함수가 되는 함수를 말한다. 따라서 아래와 같이 전개할 수 있다.
{ϕ∘ϕ−1:(z≠0)→(z≠0).  ϕ(ϕ−1(x:y:z))=ϕ(xz,yz)=(xz:yz:1)ϕ−1∘ϕ:ϕ−1(ϕ(x,y))=ϕ−1(x:y:1)=(x,y)\begin{cases} \phi\circ\phi^{-1}:(z\neq0)\rightarrow (z\neq0).\;\phi(\phi^{-1}(x:y:z))=\phi(\frac{x}{z},\frac{y}{z})=(\frac{x}{z}:\frac{y}{z}:1) \\ \phi^{-1}\circ \phi:\phi^{-1}(\phi(x,y))=\phi^{-1}(x:y:1)=(x,y) \end{cases}

Exercise 1.4.11

l={(x,y)∈C2:ax+by+c=0}⊂C2l=\{(x,y)\in \mathbb{C}^2:ax+by+c=0\}\subset \mathbb{C}^2라 하고 이 때 a,b≠0a,b\neq0이라고 하자.
만약 ∣x∣→∞|x|\rightarrow \infty면 ∣y∣→∞|y|\rightarrow \infty를 만족한다(∵y=−abx−cb\because y=-\frac{a}{b}x-\frac{c}{b}).

Exercise 1.4.12

이번엔 b≠0b\neq0일 경우를 살펴본다. l={(x,y)∈C2:ax+by+c=0}l=\{(x,y)\in \mathbb{C}^2:ax+by+c=0\}이므로 이를 정리하면 by=−ax−cby=-ax-c가 되므로 (x:y:1)∼(bx:by:b)∼(bx:−ax−c:b)(x:y:1)\sim(bx:by:b)\sim(bx:-ax-c:b)가 된다. 따라서 ϕ(l)\phi(l)은 아래와 같다.
ϕ(l)={(bx:−ax−c:b):x∈C}⊂PC2={(0:−c:b)}∪{(bx:−ax−c:b):x∈C∗}\begin{align*} \phi(l)&=\{(bx:-ax-c:b):x\in\mathbb{C}\}\subset \mathbb{P}^2_\mathbb{C}\\ &=\{(0:-c:b)\}\cup\{(bx:-ax-c:b):x\in \mathbb{C}^{*}\} \end{align*}
만약 ∣x∣→∞|x|\rightarrow \infty라면 (bx:−ax−c:b)→(b:−a:0)(bx:-ax-c:b)\rightarrow (b:-a:0)이 된다.

Definition

(a:b:c)∈PC2(a:b:c)\in\mathbb{P}^2_\mathbb{C}를 (a,b,c)(a,b,c)에 대한 동차좌표(homogeneous coordinate)라 한다. 이 때 이 표현식(representation)은 유일하지 않다(예를들어 (1:2:3)(1:2:3)은 (2:4:6)(2:4:6)과 같은 값을 가리킨다).

Definition

만약 어떤 다항식의 모든 항이 같은 총차수(total degree)를 갖는다면 이를 동차다항식(homogeneous polynomial)이라고 한다.

Example

x2+xy−z2x^2+xy-z^2은 x2x^2은 2차, xyxy도 2차, z2z^2도 2차이므로 총차수(total degree)가 22인 동차(homogeneous) 다항식이다.

Exercise 1.4.18

P(x,y,z)=x2+2y+2zP(x,y,z)=x^2+2y+2z는 동차다항식이 아니다(non-homogeneous)(∵\because x2x^2은 22차지만 2y2y와 2z2z는 11차이다). 이 때 동차관계