///
Search
📄

Chapter 1.1: Conics over the Reals

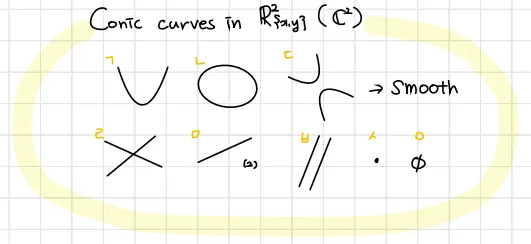
본 문서에선 판별식을 통해 이차식(conic)의 종류를 살펴본다. 후술하듯 이차식은 (ㄱ)포물선, (ㄴ)타원, (ㄷ)쌍곡선, (ㄹ)한점에서 만남, (ㅁ)겹치는 한개의 선, (ㅂ)평행한 두 선, (ㅅ)한 점, (ㅇ)공집합으로 총 8개 클래스로 이루어져있다. 정리하면 이번챕터에선 판별식을 통해 이차식의 8개 클래스를 분류해볼 것이다.
note P(x,y)P(x,y)는 이차다항식을 의미한다.
C={(x,y)∈R2:P(x,y)=0}=:V(P)C=\{(x,y)\in \mathbb{R}^2: P(x,y)=0\} =: V(P)로 정리할 수 있으며 V(P)V(P)는 vertices로 공통근들을 의미한다.
이차식은 아래 8가지로 분류된다. 이차곡선(Conic curve)은 8가지 중 스무스함수인 위쪽의 4가지(포물선, 원, 타원, 쌍곡선)을 의미한다.
이차식의 기본형은 아래와 같다.
P(x,y)=ax2+bxy+cy2+dx+ey+fP(x,y)=ax^2+bxy+cy^2+dx+ey+f
여기서 yy가 없이 xx만 있을 경우 DD를 판별식으로 활용할 수 있다.
위 식을 xx에 대한 식으로 정리하면 P(x,y)=ax2+(by+d)x+(cy2+ey+f)=0P(x,y)=ax^2+(by+d)x+(cy^2+ey+f)=0로 표현할 수 있다. 위 식에서 근의 공식을 사용해 xx를 구하면 아래와 같다.

Exercise 1.1.13

x=−(by+d)±(by+d)2−4a(cy2+ey+f)2ax=\frac{-(by+d)\pm\sqrt{(by+d)^2-4a(cy^2+ey+f)}}{2a}
따라서 xx에 대한 판별식 △x(y)\triangle_x (y)는 yy에 대한 함수이며 아래와 같이 정리된다.

Exercise 1.1.14

△x:=(by+d)2−4a(cy2+ey+f)=(b2−4ac)y2+(2bd−4ae)y+(d2−4af)∈R[y]\begin{align*} \triangle_x &:= (by+d)^2-4a(cy^2+ey+f) \\ &=(b^2-4ac)y^2+(2bd-4ae)y+(d^2-4af) \in \mathbb{R}[y] \end{align*}

Exercise 1.1.15

1.
만약 △x(y0)<0\triangle_x(y_0)<0이면 ⇒\Rightarrow y=y0y=y_0에 대해 ∄(x,y)∈V(P)\nexists(x,y) \in V(P) (근이 없다).
2.
만약 △x(y0)=0\triangle_x(y_0)=0이면 ⇒\Rightarrow y=y0y=y_0에 대해 ∃!(x,y)∈C\exists!(x,y) \in C (중근 (−by02a,y0)(-\frac{by_0}{2a},y_0)을 가진다).
3.
만약 △x(y0)>0\triangle_x(y_0)>0이면 ⇒\Rightarrow y=y0y=y_0에 대해 ∃  exactly  2  (x,y)∈C\exist\;exactly\;2\;(x,y) \in C (2개의 근을 가진다).

Exercise 1.1.16

근이 존재할 조건 {y∈R:△x(y)≥0}\{y\in\mathbb{R}:\triangle_x(y)\geq 0\}을 가정하여 고려한다.
먼저 b2−4ac=0b^2-4ac=0일 때를 살펴본다.
이를 판별식에 대입하면 아래와 같이 전개된다.
△x:=(b2−4ac)y2+(2bd−4ae)y+(d2−4af)=(2bd−4ae)y+(d2−4af)≥0\begin{align*} \triangle_x &:= (b^2-4ac)y^2+(2bd-4ae)y+(d^2-4af) \\ &=(2bd-4ae)y+(d^2-4af) \geq 0 \end{align*}
여기서 (2bd−4ae)(2bd-4ae)가 00보다 클 때, 00보다 작을 때, 00과 같을때 이렇게 세가지 경우를 고려해볼 수 있다. 먼저 00보다 클 때를 먼저 고려해본다.
1.
△x(y)=(2bd−4ae)y+(d2−4af)≥0\triangle_x(y)=(2bd-4ae)y+(d^2-4af)\geq0 ⇔(2bd−4ae)y≥−(d2−4af)\Leftrightarrow (2bd-4ae)y\geq -(d^2-4af) ⇔y≥−d2−4af2bd−4ae=4af−d22bd−4ae\Leftrightarrow y\geq -\frac{d^2-4af}{2bd-4ae}=\frac{4af-d^2}{2bd-4ae}
2.
yy값에 대해 경계(boundary)가 생기며 이에 해당하는 이차곡선은 포물선(parabola)이다.
00보다 작을 때도 같은 결론이 나며 정리하면 (2bd−4ae)(2bd-4ae)가 00보다 크거나 같을 때 포물선이다.
다음은 2bd−4ae=02bd-4ae=0일 때를 고려한다.
b2−4ac=0⇒b2=4ac,  2bd−4ae=0⇒d=2aebb^2-4ac=0 \Rightarrow b^2=4ac,\; 2bd-4ae=0 \Rightarrow d=\frac{2ae}{b}
△x(y)=(2bd−4ae)y+(d2−4af)=d2−4af≥0\triangle_x(y)=(2bd-4ae)y+(d^2-4af)=d^2-4af \geq 0
1.
d2−4af>0⇒x=−(by+d)±d2−4af2ad^2-4af>0 \Rightarrow x=\frac{-(by+d)\pm\sqrt{d^2-4af}}{2a}, 즉 평행한 두 선(ㅂ에 해당)
2.
d2−4af=0⇒x=−(by+d)2ad^2-4af=0 \Rightarrow x=\frac{-(by+d)}{2a}, 즉 겹치는 한개의 선(ㅁ에 해당)

Exercise 1.1.17

이번엔 b2−4ac<0b^2-4ac<0일 때를 살펴본다. 이 때 아래 세가지 경우를 고려할 수 있다.
1.
{y:△x(y)≥0}=∅\{y:\triangle_x(y)\geq0 \}=\empty △x(y)\triangle_x(y)가 0보다 커야 근이 존재하는데 이를 만족하는 yy가 존재하지 않으므로 근이 될 수 있는 좌표가 없음을 의미한다. 따라서 C=∅C=\empty
2.
{y:△x(y)≥0}={y0}\{y:\triangle_x(y)\geq0\}=\{y_0\} 만족하는 yy가 y0y_0 하나 존재하므로(중근) C={(x0,y0)}C=\{(x_0,y_0)\}이고 x0=−by0+d2ax_0=-\frac{by_0+d}{2a}
3.
α,β∈R,  (α<β)\alpha,\beta \in \mathbb{R},\;(\alpha<\beta)에 대해 {y:△x(y)≥0}={y:α≤y≤β}=[α,β]\{y:\triangle_x(y)\geq0\}=\{y:\alpha \leq y \leq \beta\}=[\alpha,\beta]인 α,β\alpha, \beta가 존재한다. 즉 yy의 양측 경계값(boundary)가 존재한다. 이차곡선 중 상한과 하한이 존재하는것은 타원이 유일하므로 CC는 타원(ellipse)다.

Exercise 1.1.18

마지막으로 b2−4ac>0b^2-4ac>0일 때를 살펴본다. 판별식 △x(y)\triangle_x(y)의 최고차항의 계수가 양수인 경우이므로 아래 세가지 경우를 고려할 수 있다. 여기서 판별식 D={y∈R:△x(y)≥0}D=\{y\in\mathbb{R}:\triangle_x(y)\geq 0\}에 해당한다.
1.
D=RD=\mathbb{R}이고 △x(y)≠0\triangle_x(y)\neq0면 CC는 쌍곡선(hyperbola)이다.
판별식이 0이 아님
2.
D=RD=\mathbb{R}이고 {y∈R:△x(y)=0}={y0}\{y\in \mathbb{R}:\triangle_x(y)=0\}=\{y_0\}면 CC는 한점에서 만난다. (이차곡선 중 ㄹ에 해당)
판별식이 한점에서 만남
3.
D=(−∞,α]∪[β,∞)D=(-\infty,\alpha]\cup[\beta,\infty)면 CC는 쌍곡선(hyperbola)이다.
판별식이 두 점에서 만남

Theorem

CC가 스무스(smooth)함수일 때
V(P)
판별식
타원(ellipse)
b2−4ac<0b^2-4ac <0
쌍곡선(hyperbola)
b2−4ac>0b^2-4ac >0
포물선(parabola)
b2−4ac=0b^2-4ac =0