Search

HybrIK: A Hybrid Analytical-Neural Inverse Kinematics Solution for 3D Human Pose and Shape Estimation

리뷰완료날짜
2023/03/26
리뷰어
카테고리
컴퓨터비전
출판
CVPR 2021
파일
https://arxiv.org/abs/2011.14672
태그
HPS

요약

Model-base의 3D 관절 및 형태(Human pose and shape, 이하 HPS)은 몇개의 파라미터를 이용해서 사람의 3D 메쉬를 추정하는 연구이다. 그러나 이런 파라미터의 경우 비선형성을 가지며 이미지와 모델 사이의 관계를 추정하는데 어려움이 있다. 이에 비해 3D 키포인트를 예측하는 모델은 비교적 정확하게 3D 키포인트는 추정할 수 있으나 관절사이의 관절을 고려하지 않기 때문에 비현실적인 키포인트가 추정될 수 있다는 한계가 있다. 본 연구에서는 3차원 키포인트와 메쉬 사이의 간극을 메우는 방식을 제안한다. 이를 위해 hybrid inverse kinematics solution(HybrIK)를 제안하며 이는 3차원 조인트와 바디파츠간의 회전행렬 바로 추정하여 3차원 바디메쉬를 생성하는 방법이다. 본 연구에서는 회전행렬을 swing을 담당하는 회전행렬과 twist 회전행렬의 곱으로 분리하여 네트워크가 두 개의 회전행렬을 추정한 후 곱하여 전체 행렬을 만드는 방식으로 과정을 진행하였다. swing 회전행렬은 Yaw와 Pitch에 해당하며 이는 3D 키포인트를 이용하여 구하였고 twist는 Roll에 해당하며 이는 이를 위한 네트워크를 따로 구성하였다.

Introduction

3D 키포인트를 추정하는 연구는 휴먼바디모델의 사용 유무에 따라 Model-based 방식과 Model-free 방식으로 나뉘어지는데 여기서 Model-based 방식의 경우 크게 optimization-based 방식과 learning-based 방식으로 나뉘어 진다.
optimization-based 방식의 경우 키포인트 기준으로 바디의 shape과 pose를 맞추는 방식을 말하며 대표적으로 SMPLify가 있다. 주로 2차원이나 3차원 관절에 파라미터를 맞추는데 이는 non-convex하고 시간이 오래걸리는 단점이 있다. 뿐만 아니라 초기값에 민감하다.
learning-based 방식의 경우 주로 딥러닝 모델을 활용하여 파라미터를 추정하는데 이는 위 문제를 어느정도 해결할 수 있지만 mapping function을 설계하고 모델을 학습시키는 부분이 어려운 부분이 될 수 있다.
Model-free 방식의 경우 3D 키포인트를 volumetric heatmap으로 표현함으로써 비약적인 성능 향상을 이루었다. 그러나 사람의 뼈의 길이나 각 관절 사이의 관계를 고려하여 모델링하지 않기 때문에 비현실적인 비율이나 자세가 나올 수 있다는 한계가 있다.
본 연구에서는 3차원 관절값과 kinematic solution의 간극을 최소화하는 방식을 제안하여 3차원 관절인식과 메쉬 추정에 관한 성능을 높이고자 하였다. 이를 위해 회전행렬을 swing와 twist로 분리하였다. 3차원 관절위치를 이용하여 swing 회전행렬을 계산하고 모델로 부터 twist 회전행렬을 추정한 후 다시 결합하여 바디 키포인트의 회전값을 계산한다. 이를 통해 이전 연구들과 달리 추가적인 optimization 과정이 필요없게 된다. 특히 HybrIK의 경우 모든 함수가 미분이 가능하며 때문에 end-to-end로 3차원 관절과 사람의 메쉬를 동시에 훈련할 수 있다. 게다가 본 연구는 기존 3차원 관절인식 모델에 적용하여 성능을 높인 결과를 보여준다.

Method

Preliminary

Kinematics에 관한 기본적인 내용은 아래 링크를 참고!
•
Forward Kinematics (FK)
Forward Kinematics의 경우 결과 포즈 Q={qk}k=1K\mathbf{Q}=\{q_k\}^{K}_{k=1}, 기본 포즈 템플릿 T={tk}k=1K\mathbf{T}=\{t_k\}^{K}_{k=1}, 그리고 관절 kk와 그의 부모관절 pa(k)pa(k)사이의 회전행렬 R{Rpa(k),k}k=1K\mathbf{R}\{R_{pa(k),k}\}^{K}_{k=1}라 할 때, 아래와 같이 표현할 수 있다.
Q=FK(R,T)\mathbf{Q}=\mathbf{FK(R,T)}
정리하면 기본 템플릿과 회전행렬을 넣어 결과포즈를 산출하는 함수가 FK\mathbf{FK}이다(IK\mathbf{IK}는 반대로 목표포즈와 기본템플릿을 넣으면 회전행렬을 산출).
qk=Rk(tk−tpa(k))+qpa(k)q_k=R_k(t_k-t_{pa(k)})+q_{pa(k)}
KK는 관절의 개수이며 qk∈R3q_k \in \R_3은 템플릿 T\mathbf{T}의 kk번째 관절 위치이다. 위 수식은 k번째 관절의 위치는 k번째 템플릿 관절과 그의 부모 템플릿 관절위치를 통해 벡터를 구하고 이에 회전행렬을 곱하여 부모 관절의 위치에 더하면 구하고자 하는 관절의 위치가 나오는 것을 보여준다.
FK\mathbf{FK}는 템플릿 바디파트를 루트관절(root joint)부터 리프관절(leaf joint)까지 재귀적으로 회전하여 관절 위치를 조정한다. Rk∈SO(3)R_k \in \mathbb{SO}(3)는 kk번째 관절의 global 회전행렬이며 아래와 같이 재귀적으로 계산된다.
Rk=Rpa(k)Rpa(k),k⋅R_k = R_{pa(k)}R_{pa(k),k\cdot}
즉, 루트조인트 부터 시작하여 부모조인트의 회전값과 그에 상대적인 현재 조인트의 회전값을 재귀적으로 곱하여 타겟 조인트까지 반복하여 구한것이 타겟조인트의 global 회전행렬이 된다. 부모관절이 없는 루트관절의 경우 q0=t0q_0=t_0 이 된다.
•
Inverse Kinematics (IK)
IK는 FK의 역으로 아래와 같이 표현된다.
R=IK(P,T)\mathbf{R=IK(P,T)}
IK\mathbf{IK}는 일반적으로 오차가 있지만 이상적인 상황은 아래와 같은 수식이 성립한다. 특히 후술하겠지만 이는 ∥pk−ppa(k)∥=∥tk−tpa(k)∥\Vert p_k - p_{pa(k)} \Vert = \Vert t_k - t_{pa(k)} \Vert 가 성립해야한다.
pk−ppa(k)=Rk(tk−tpa(k))∀1≤k≤Kp_k-p_{pa(k)}=R_k(t_k-t_{pa(k)})\quad \forall 1\leq k \leq K
FK\mathbf{FK}와 마찬가지로 부모조인트가 없는 루트관절의 경우 p0=t0p_0=t_0가 된다. IK\mathbf{IK}는 ill-posed문제(근이 1개만 존재하지 않는 문제. 근이 없거나 무한한 경우)를 가진다. 최근엔 인공신경망을 이용하여 IK\mathbf{IK}문제를 해결하는 연구들도 진행되고 있다.

Hybrid Analytical-Neural Inverse Kinematics

•
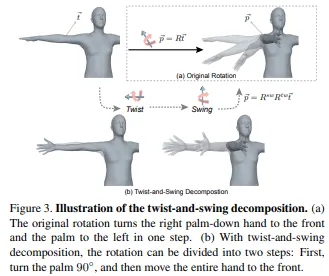
Twist-and-Swing Decomposition
회전행렬 R∈SO(3)R \in \mathbb{SO(3)}은 twist 회전행렬 RtwR^{tw}와 swing 행렬 RswR^{sw}로 분리할 수 있다. 템플릿 바디파트 벡터를 t⃗\vec{t}, 타겟 벡터를 p⃗\vec{p}, 그리고 결과 회전행렬을 RR이라고 하면 아래의 수식으로 표현 할 수 있다.
R=D(p⃗,t⃗,ϕ)=Dsw(p⃗,t⃗)Dtw(t⃗,ϕ)=RswRtwR=\mathcal{D}(\vec{p},\vec{t},\phi)=\mathcal{D}^{sw}(\vec{p},\vec{t})\mathcal{D}^{tw}(\vec{t},\phi)=R^{sw}R^{tw}
여기서 ϕ\phi는 twist각이며 인공신경망을 통해서 구할수 있고 회전행렬 R은 p⃗=Rt⃗\vec{p}=R\vec{t}를 만족한다.
◦
Swing
swing 회전행렬은 회전축 n⃗\vec{n}을 가지며 이는 t⃗\vec{t}와 p⃗\vec{p}의 법선벡터이므로 아래 수식과 같이 표현할 수 있고,
n⃗=t⃗×p⃗∥t⃗×p⃗∥\vec{n}={\vec{t}\times\vec{p}\over\Vert\vec{t}\times\vec{p}\Vert}
swing 각 α\alpha는 외내적 공식을 이용하면 아래와 같이 표현할 수 있다.
cos⁡α=t⃗⋅p⃗∥t⃗∥∥p⃗∥,sin⁡α=∥t⃗×p⃗∥∥t⃗∥∥p⃗∥\cos\alpha={\vec{t}\cdot\vec{p} \over \Vert\vec{t}\Vert\Vert\vec{p}\Vert}, \quad \sin\alpha={\Vert\vec{t}\times\vec{p}\Vert \over \Vert\vec{t}\Vert\Vert\vec{p}\Vert}
이를 Rodrigues formula를 이용하면 아래 수식으로 표현할 수 있다.
Rsw=Dsw(p⃗,t⃗)=I+sin⁡α[n⃗]×+(1−cos⁡α)[n⃗]×2R^{sw}=\mathcal{D}^{sw}(\vec{p},\vec{t})=\mathcal{I}+\sin\alpha[\vec{n}]_\times+(1-\cos\alpha)[\vec{n}]^2_\times
[n⃗]×[\vec{n}]_{\times}은 n⃗\vec{n}의 반대각행렬이고 I\mathcal{I}는 3×33\times3 크기의 항등행렬이다.
◦
Twist
twist 회전행렬은 t⃗\vec{t}가 축이 되고 ϕ\phi각도 만큼 회전하며 twist 회전행렬 RtwR^{tw}를 아래와 같이 표현할 수 있다.
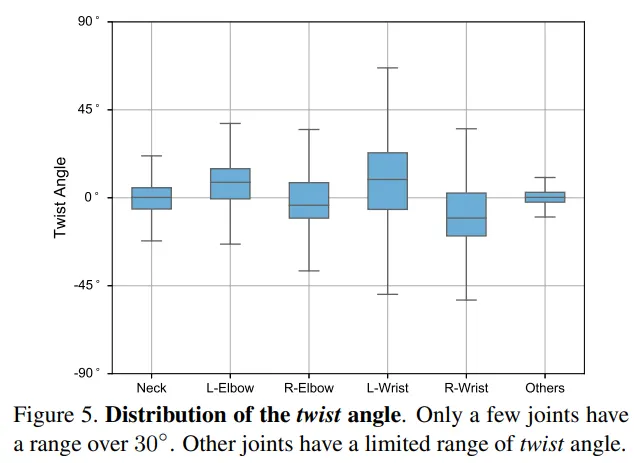
Rtw=Dtw(t⃗,ϕ)=I+sin⁡ϕ∥t⃗∥[t⃗]×+(1−cos⁡ϕ)∥t⃗∥2[t⃗]×2R^{tw}=\mathcal{D}^{tw}(\vec{t},\phi)=\mathcal{I}+{\sin\phi\over\Vert\vec{t}\Vert}[\vec{t}]_\times + {(1-\cos\phi)\over\Vert\vec{t}\Vert^2}[\vec{t}]^2_\times
Dsw\mathcal{D}^{sw}와 Dtw\mathcal{D}^{tw}는 완전히 미분이 가능한 함수이기 때문에 twist-and-swing decomposition을 훈련과정에 포함해도 문제가 없다. 신경망이 twist각에 대해선 학습해야 하지만 나머지는 훈련할 필요가 없어 문제를 단순하게 만들 수 있다. 특히 twist각은 각의 다양성의 범위가 작은범위로 제한되어 있기 때문에 mapping fuction을 학습하기가 더 쉬워진다.
•
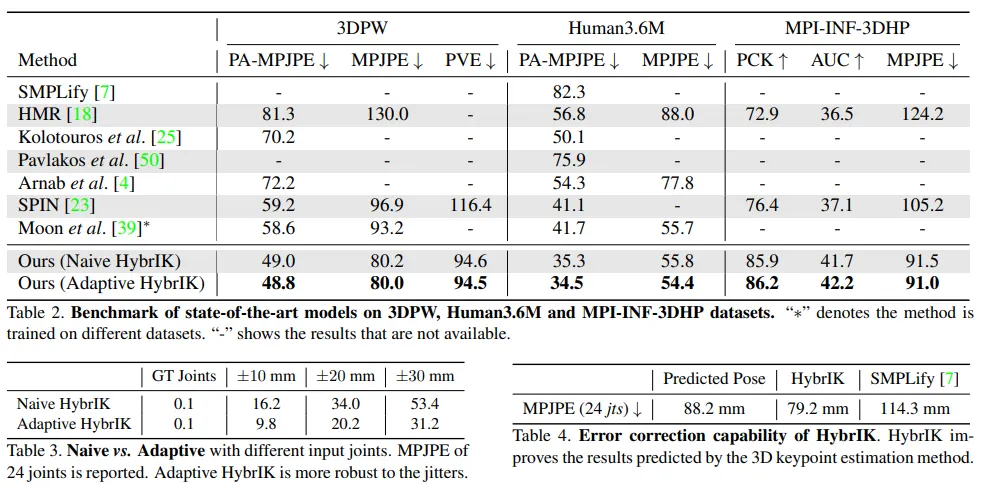
Naive HybrIK
위에 언급한 식을 이용하여 전개하면 아래와 같은 수식이 구해진다.
Rk=Rpa(k)Rpa(k),kR_k=R_{pa(k)}R_{pa(k),k}
pk−Ppa(k)=Rk(tk−tpa(k))∀1≤k≤Kp_k-P_{pa(k)}=R_k(t_k-t_{pa(k)}) \quad \forall 1\leq k \leq K
pk−ppa(k)=Rk(tk−tpa(k))=(Rpa(k)Rpa(k),k)(tk−tpa(k))∴Rpa(k)−1(pk−ppa(k))=Rpa(k),k(tk−tpa(k))\begin{align*} p_k-p_{pa(k)}=R_k(t_k-t_{pa(k)}) \\ =(R_{pa(k)}R_{pa(k),k})(t_k-t_{pa(k)}) \\ \therefore R^{-1}_{pa(k)}(p_k-p_{pa(k)}) = R_{pa(k),k}(t_k-t_{pa(k)}) \end{align*}
여기서 pk⃗=Rpa(k)−1(pk−ppa(k))\vec{p_k}=R^{-1}_{pa(k)}(p_k-p_{pa(k)})라 하고 tk⃗=tk−tpa(k)\vec{t_k}=t_k-t_{pa(k)}라 하면 pk⃗=R⋅tk⃗\vec{p_k}=R\cdot\vec{t_k}를 만족하므로 회전행렬의 조건을 만족한다. 따라서 아래 식이 성립한다.
∴Rpa(k),k=D(pk⃗,tk⃗,ϕk)\therefore R_{pa(k),k}=\mathcal{D}(\vec{p_k},\vec{t_k},\phi_k)
회전행렬은 othogonal하기 때문에 역행렬이 전치행렬과 같다. 따라서 Rpa(k)−1=Rpa(k)TR^{-1}_{pa(k)}=R^T_{pa(k)}가 성립하게 된다. 이를 Naive HybrIK 알고리즘이라 하며 정리하면 아래와 같다.
•
Adaptive HybrIK
Naive HybrIK가 효율적인 방식이지만 위에서 언급했듯이 ∥pk−ppa(k)∥=∥tk−tpa(k)∥\Vert p_k - p_{pa(k)} \Vert = \Vert t_k - t_{pa(k)} \Vert라는 가정이 만족되어야 한다. 그러나 3D 관절 위치를 추정할 때, 템플릿 관절과 같은 크기의 관절 길이를 가지지 않는다. 따라서 수식으로 표현하면 아래와 같다.
pk−ppa(k)=Rk(tk−tpa(k))+ϵk⃗p_k-p_{pa(k)}=R_k(t_k-t_{pa(k)})+\vec{\epsilon_k}
ϵ⃗\vec{\epsilon}은 kk번째 관절의 에러이며 pk−ppa(k)p_k-p_{pa(k)}와 같은 방향의 벡터이며 크기는 ∥ϵ⃗∥=∥pk−ppa(k)∥−∥tk−tpa(k)∥\Vert \vec{\epsilon}\Vert=\Vert p_k-p_{pa(k)}\Vert - \Vert t_k-t_{pa(k)}\Vert를 만족한다. 이 에러를 reconstruction error라 하고 이를 계산하기 위해 입력 포즈 PP와 reconstructed 포즈를 QQ라 했을 때 Q=FK(R,T)=FK(IK(P,T),T)\mathbf{Q=FK(R,T)=FK(IK(P,T),T)}이며 아래 수식으로 정리할 수 있다.
∥P−Q∥⇔∑k=1K∥pk−qk∥\Vert P-Q\Vert \Leftrightarrow\sum_{k=1}^{K}{\Vert p_k-q_k \Vert}
pk−qk=ppa(k)−qpa(k)+ϵ⃗k=ppa2(k)−qpa2(k)+ϵ⃗pa(k)+ϵ⃗k=...=∑i∈A(k)ϵ⃗i\begin{align*} p_k-q_k = p_{pa(k)}-q_{pa(k)}+\vec{\epsilon}_k \\ =p_{pa^2(k)}-q_{pa^2(k)}+\vec{\epsilon}_{pa(k)}+\vec{\epsilon}_k \\ = ...=\sum_{i\in A(k)}{\vec{\epsilon}_i} \end{align*}
pa2(k)pa^2(k)는 pa(k)pa(k)의 부모인덱스고 A(k)A(k)는 kk번째 관절의 부모관절의 인덱스 집합이다. 루트관절에서 끝으로 갈 수록 에러가 축적되게 된다.
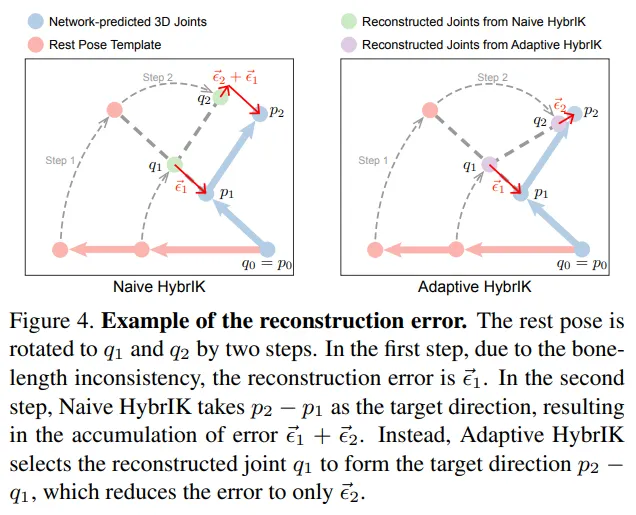
이 문제를 해결하기 위해 본 연구에서는 Adaptive HybrIK를 제안했다. 아래 논문 그림 참고
Adaptive HybrIK는 HybrIK과 q1q_1을 조정하는 과정은 똑같으나 그 다음 과정에서 p2−q1p_2-q_1방향으로 만드므로써 ϵ⃗2\vec{\epsilon}_2를 줄여 정확도를 향상시켰다. 알고리즘의 전체과정은 아래와 같다.

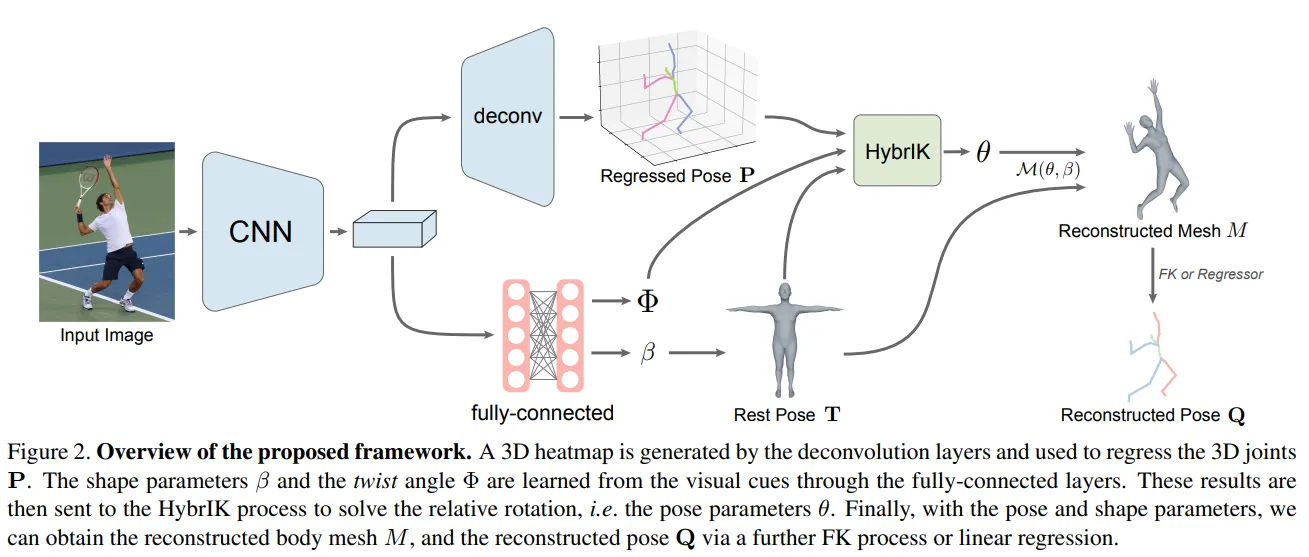
Learning Framework

전체 프레임워크는 위 그림과 같다.
1.
신경망으로 부터 3D 관절값 PP와 twist각 Φ\Phi, shape parameter β\beta를 구한다.
2.
shape parameter를 SMPL모델에 넣어 템플릿 T를 구한다.
3.
P,T,Φ\mathbf{P, T, \Phi}를 입력값으로 HybrIK를 이용하여 R\mathbf{R}을 구한다.
4.
SMPL 함수 M(θ,β)\mathcal{M}(\theta, \beta)를 이용하여 최종적으로 pose Q\mathbf{Q}를 구한다.

3D Keypoint Estimation

ResNet을 backbone으로 활용하였고 여기에 1×11\times 1 convolution을 통해 3개의 deconvolution layer를 추가하여 3D Heatmap을 추정하도록 설계하였다. 그 후 soft-argmax 함수를 통해 최종적으로 3D 관절위치를 추정하였다.
Ltw=1K∑k=1K∥pk−p^k∥1\mathcal{L}_{tw}={1\over{K}}\sum_{k=1}^{K}{\Vert p_k-\hat{p}_k\Vert_1}

Twist Angle Estimation

스칼라값인 ϕk\phi_k를 바로 추정하지 않고 2차원 벡터 (cϕk,sϕk)(c_{\phi_k},s_{\phi_k})를 추정한다. cϕkc_{\phi_k}는 cos⁡ϕk\cos{\phi_k}, sϕks_{\phi_k}는 sin⁡ϕk\sin{\phi_k}를 의미한다.
Ltw=1K∑k=1K∥(cϕk,sϕk)−(cos⁡ϕ^k,sin⁡ϕ^k)∥2\mathcal{L}_{tw}={1\over K}\sum_{k=1}^{K}{\Vert(c_{\phi_k},s_{\phi_k})-(\cos{\hat{\phi}_k},\sin{\hat{\phi}_k})\Vert_2}

Collaboration with SMPL

SMPL관련 파라미터 손실함수는 아래와 같다.
Lshape=∥β−β^∥2\mathcal{L}_{shape}=\Vert \beta-\hat{\beta}\Vert_2
Lrot=∥θ−θ^∥2\mathcal{L}_{rot}=\Vert \theta-\hat{\theta}\Vert_2
최종 손실함수식은 아래와 같다.
L=Lpose+μ1Lshape+μ2Lrot+μ3Ltw\mathcal{L}=\mathcal{L}_{pose}+\mu_1\mathcal{L}_{shape}+\mu_2\mathcal{L}_{rot}+\mu_3\mathcal{L}_{tw}

Implementation Details

본 연구에서는 ResNet-23를 백본으로 활용하였고 이는 ImageNet pre-trained weight를 활용하였다. ResNet의 출력은 2개의 브랜치로 나뉘어 첫번째 브랜치는 3D heatmap을 추정하고 두번째 브랜치는 shape parameter β∈R10 \beta\in\mathbb{R}^{10}와 twist 각도 Φ∈R46\Phi\in\mathbb{R}^{46}를 추정한다(Φ\Phi는 2×232\times 23이므로). 입력 사이즈는 256×192256 \times 192이며 learning rate는 1×10−31 \times 10^{-3}을 초기값으로 주고 90 에포크 부터 120 에포크 사이는 factor를 10으로 하였다. 옵티마이저로 Adam을 사용하였고 총 140에포크로 학습을 돌렸으며 배치사이즈는 32로 μ1=1\mu_1=1, μ2=μ3=1×10−2\mu_2=\mu_3=1\times 10^{-2}로 하이퍼파라미터를 설정하였다. 루트 위치의 경우 RootNet (문경식 박사님 논문)을 사용하여 추정하였다.