///
Search
📄

2.1 Basic Notions

복소수 집합은 i2=−1i^2=-1을 사용하여 실수 R\mathbb{R}인 숫자로 표현된다. 복소수는 기하적인 관점에서 실수 순서쌍 (x,y)(x,y)로 정의된다. 복소수 집합 C\mathbb{C}를 표현하면 아래와 같다.
C={(x,y)∣x,y∈R}\mathbb{C}=\{(x,y)|x,y\in \mathbb{R}\}
복소수 z=(x,y)z=(x,y)에 대해 zz의 실수부는 Re(z)\sf{Re}\it{(z)}, 허수부는 Im(z)\sf{Im}\it{(z)}로 표기한다. 실수의 집합은 임의의 실수 xx에 대해 x↔(x,0)x\leftrightarrow(x,0)인 C\mathbb{C}의 부분집합이다.
또한 C \mathbb{C}는 컴포넌트와이즈(componentwise)하다
(x,y)+(s,t)=(x+s,y+t)(x,y)+(s,t)=(x+s,y+t)
만약 kk가 실수면 아래와 같이 스칼라곱을 정의할 수 있다.
k⋅(x,y)=(kx,ky)k\cdot (x,y)=(kx,ky)
이런 프레임워크에서 복소수 (x,y)(x,y)는 x+yix+yi로 아래와 같이 표현할 수 있다.
(x,y)=(x,0)+(0,y)=x(1,0)+y(0,1)=x+yi\begin{align*} (x,y)&=(x,0)+(0,y) \\ &=x(1,0) + y(0,1) \\ &=x+yi \end{align*}
x+yix+yi는 복소수의 카테시안 폼(Cartesian form; 데카르트 형식)이라 한다. 이런 형태는 복소수의 산술분야에 유용하게 사용되지만 약간 어색할 수 있다. 본 문서에선 복소수를 주로 zz나 ww같은 한개짜리 소문자로 표현할 것이다. 따라서 z=x+yiz=x+yi는 zz가 평면위의 (x,y)(x,y)점과 일치한다는 것을 말한다.
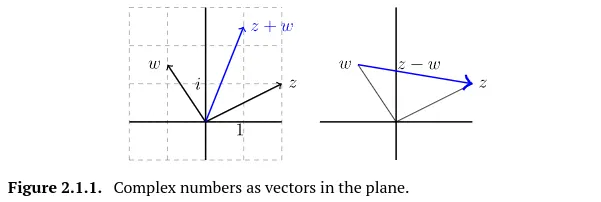
복소수를 벡터로써 바라보는것은 때론 매우 유용하며, 복소수의 덧셈은 평면위의 벡터의 덧셈과 같으며 스칼라 곱 또한 벡터의 스칼라 곱과 같다. 예를 들어 아래 그림은 z=2+iz=2+i와 w=−1+1.5iw=-1+1.5i의 덧셈인 z+w=1+2.5iz+w=1+2.5i를 벡터로 표현한 그림이다. 복소수 z−wz-w는 ww에서 zz로 가는 벡터로 표현할 수 있다.
i2=−1i^2=-1임을 이용해서 복소수의 곱도 정의할 수 있다.
(x+yi)⋅(s+ti)=xs+ysi+xti+yti2=(xs−yt)+(ys+xt)i\begin{align*}(x+yi)\cdot(s+ti)&=xs+ysi+xti+yti^2 \\ &=(xs-yt)+(ys+xt)i\end{align*}
z=x+yiz=x+yi의 모듈러스(modulus)는 ∣z∣|z|로 표현하고 아래와 같이 계산한다.
∣z∣=x2+y2|z|=\sqrt{x^2+y^2}
∣z∣|z|는 (0,0)(0,0)과 zz사이의 유클리드 거리(Euclidean distance)와 같다.
z=x+yiz=x+yi의 켤레(conjugate)는 zˉ\bar{z}로 표기하고 아래와 같이 허수부의 부호를 바꾼 값이다.
zˉ=x−yi\bar{z}=x-yi

Example 2.1.2. 복소수 연산

z=3-4i, w=2+7i라 하자. 이 때 두 수의 덧셈은 z+w=5+3iz+w=5+3i이고 곱셈은 아래와 같다.
z⋅w=(3−4i)(2+7i)=6+28−8i+21i=34+13i\begin{align*} z\cdot w&=(3-4i)(2+7i)\\ &=6+28-8i+21i \\ &=34+13i \end{align*}
스칼라곱, 모듈러스, 켤레의 곱은 아래와 같다.
4z=12−16i∣z∣=32+(−4)2=5zw‾=34−13i\begin{align*} &4z=12-16i \\ &|z|=\sqrt{3^2+(-4)^2}=5 \\ &\overline{zw}=34-13i \end{align*}