///
Search
📄

3.2 Inversion

반전(inversion)변환은 어떤 원에 대해 대칭인 점으로 보내는 방법을 말한다. 이 변환은 비유클리드 기하학의 변환을 시각화하는데 중요한 역할을 수행하며, 본 섹션에선 이 내용에 관한 기초를 다룬다.
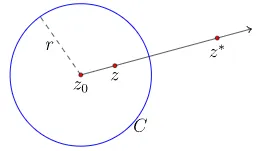
어떤 CC가 반지름이 rr이고 중심이 z0z_0인 원이라고 하자. 원 CC에 대한 반전(inversion)변환은 z0z_0가 아닌 점 zz를 다음과 같이 정의된 z∗z^*로 보내는 변환을 말한다.
먼저 z0z_0부터 시작하고 zz를 지나는 선(ray)를 만든다. 이 때, z∗z^*를 이 선 위를 지나고 아래 방정식을 만족하는 유일점(unique point)라 하자.
∣z−z0∣⋅∣z∗−z0∣=r2|z-z_0|\cdot |z^*-z_0|=r^2
이 때 점 z∗z^*를 CC에서 zz에 대한 대칭점(symmetric point)이라고 한다.
중심이 z0z_0인 원에 대한 반전(inversion)은 z0z_0을 제외한 모든 복소수(complex number)로 구성된 집합 C−{z0}\mathbb{C}-\{z_0\}에서의 변환(transformation)이다. 원 CC에 대한 반전(inversion)변환은 by  iC(z)=z∗by\;i_C(z)=z^*로 표기한다. 다음 섹션에선 이 변환에 대해 중심점 z0z_0을 포함하는 변환으로 확장할 수 있는지 살펴볼것이다.
아래 Exercise들을 통해 반전(inversion)변환에 대한 몇가지 특징들을 살펴보자. 이 과정에서 컴파스(compass)와 자(ruler)를 이용해서 어떻게 대칭점(symmetric point)를 만들 수 있는지도 볼 것이다.
iCi_C는 원 CC의 모든점은 고정(fixes)하고, 원 내부점들은 원 바깥의 다른 원으로 대응(mapping)하며 이에 대한 역도 성립한다(원 바깥의 점은 원 내부로 매핑함). 또한 zz가 원의 중심에 가까워질수록 iC(z)i_C(z)는 원으로 부터 멀어진다.

Example 3.2.1 Inversion in the unit circle

C\mathbb{C}에서 단위원(unit circle)은 중심이 z0=0z_0=0이고 반지름 r=1r=1인 원을 말하고 S1\mathbb{S}^1로 표기한다. S1\mathbb{S}^1에 대해 00이 아닌 점 zz의 대칭점(symmetric) z∗z^*은 ∣z−z0∣⋅∣z∗−z0∣=r2|z-z_0|\cdot |z^*-z_0|=r^2에 대입하면 아래와 같은 방정식이 성립한다.
∣z∣⋅∣z∗∣=1|z|\cdot |z^*|=1
또한 zz와 z∗z^*가 모두 원점을 지나는 직선위에 있다면 z∗z^*은 zz의 크기만 키운 버전이 된다. 이땐 kk가 양의 실수(positive real number)일 때 z∗=kzz^*=kz를 만족한다. 이를 대칭점(symmetric point) 방정식에 넣으면 ∣z∣⋅∣kz∣=1|z|\cdot|kz|=1이 되고 정리하면 k=1/∣z∣2k=1/|z|^2가 된다. 따라서 z∗=(1/∣z∣2)zz^*=(1/|z|^2)z가 된다. 또한 ∣z∣2=z⋅zˉ|z|^2=z\cdot \bar{z}이므로 단위원 S1\mathbb{S}^1에 대한 반전(inverse)은 아래와 같이 정리할 수 있다.
iS1(z)=1/zˉi_{\mathbb{S}^1}(z)=1/\bar{z}
아래 공식은 임의의 원(arbitary circle)에 대한 반전(inversion)변환에 대한 식이며 몇개의 일반선형변환(general linear transformation)을 통해 단위원(unit circle)에서의 반전(inversion)변환의 결합으로 구할 수 있다.

Inversion in the circle CC centered at z0z_0 with radius rr

중심이 z0z_0이고 반지름이 rr인 원 CC에서 반전(inversion)변환은 아래와 같다.
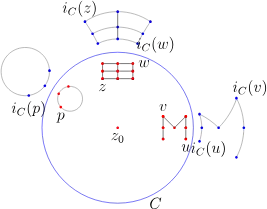
iC(z)=r2(z−z0)‾+z0i_C(z)=\frac{r^2}{\overline{(z-z_0)}} + z_0

Example 3.2.2 Inverting some figures in a circle

아래 그림과 같이 z0z_0을 중심으로 하는 원 CC에 대해 원이나 M문자나 작은 표(grid)를 반전변환하였다. 변환된 이미지들은 마치 또 다른 원 처럼 보이며 이것에 대해 증명할 것이다. 또한 원 C의 중심과 교점이 없는 직선(line)은 원으로 반전(inversion)변환 된다는 것도 보일것이다. 이에 따라 문자 M의 선분들은 원들의 호들(arcs of circles)에 매핑이 될 것이다.

Definition 3.2.3

클레인(cline)은 유클리디안 원 또는 직선을 말한다. 모든 클레인(cline)은 아래와 같은 형태의 대수방정식으로 표현이 가능하다.
czzˉ+αz+αˉzˉ+d=0cz\bar{z}+\alpha z + \bar{\alpha}\bar{z} + d=0
여기서 z=x+yiz=x+yi는 복소변수(complex variable)이고, α\alpha는 복소상수(complex constant), c,dc,d는 실수다. 만약 c=0c=0이면 방정식은 직선을 표현하고 만약 c≠0c\neq 0이고 ∣α∣2>cd|\alpha|^2>cd면 방정식은 원(circle)을 표현한다.
클레인(cline)이란 단어로 부터 직선(line)과 원(circle)은 클레인 클래스(cline class)라는 같은 일반클래스로부터 다르게 발현된것으로 이해하기 시작해야 한다.
α=a+bi\alpha=a+bi이고 z=x+yiz=x+yi라하면 클레인 방정식(cline equation) czzˉ+αz+αˉzˉ+d=0cz\bar{z}+\alpha z + \bar{\alpha}\bar{z} + d=0은 아래와 같이 쓸 수 있다.
c(x2+y2)+[ax−by+(ay+bx)i]+[ax−by−(ay+bx)i]+d=0c(x^2+y^2)+[ax-by+(ay+bx)i]+[ax-by-(ay+bx)i]+d=0
위 식을 정리하면 아래와 같다.
c(x2+y2)+2(ax−by)+d=0c(x^2+y^2)+2(ax-by)+d=0
만약 c=0c=0이라면 직선의 방정식이고, c≠0c\neq 0이면 a2+b2>cda^2+b^2>cd면 원의 방정식이다. 이를 보이기 위해 식을 아래와 같이 전개하였다.
c(x2+y2)+2ax−2by+d=0x2+2acx+y2−2bcy=−dcx2+2acx+(ac)2+y2−2bcy+(bc)2=−dc+(ac)2+(bc)2(x+ac)2+(y−bc)2=a2+b2−cdc2c(x^2+y^2)+2ax-2by+d=0 \\ x^2+\frac{2a}{c}x+y^2-\frac{2b}{c}y=-\frac{d}{c} \\ x^2+\frac{2a}{c}x+\bigg(\frac{a}{c}\bigg)^2+y^2-\frac{2b}{c}y+\bigg(\frac{b}{c}\bigg)^2 = -\frac{d}{c}+\bigg(\frac{a}{c}\bigg)^2+\bigg(\frac{b}{c}\bigg)^2 \\ \bigg(x+\frac{a}{c}\bigg)^2+\bigg(y-\frac{b}{c}\bigg)^2=\frac{a^2+b^2-cd}{c^2}
a2+b2−cd>0a^2+b^2-cd>0이므로 우항은 반지름의 제곱이 된다. 이를 요약하면 아래와 같다.

The cline equation

c,d∈Rc,d\in\mathbb{R}이고 α∈C\alpha \in \mathbb{C}로 주어졌을 때, c≠0c\neq 0이라면 클레인 방정식(cline equation)은 아래와 같고
czzˉ+αz+αˉzˉ+d=0cz\bar{z}+\alpha z + \bar{\alpha}\bar{z} + d=0
중심이 z0z_0이고 반지름이 rr이면 아래와 같다.
z0=(−Re(α)c,Im(α)c),      and      r=∣α∣2−cdc2z_0=\bigg(-\frac{\mathsf{Re}(\alpha)}{c}, \frac{\mathsf{Im}(\alpha)}{c}\bigg),\;\;\;and\;\;\; r=\sqrt{\frac{|\alpha|^2-cd}{c^2}}
이 때 ∣α∣2>cd|\alpha|^2 > cd이고 만약 c=0c=0이면 클레인 방정식은 직선이 된다.

Theorem 3.2.4

C\mathbb{C}에서 세개의 다른점을 지나는 클레인은 유일하게 존재한다.
u,v,wu,v,w가 서로다른 복소수(complex number)라고 하자. 만약 vv가 uu와 ww를 지나는 직선위의 점이고 이 직선이 이 세 점을 지나는 유일한 클레인(unique cline)이라고 하자. 세개의 점이 단일직선(single line)위에 있지 않기 때문에 세 점을 지나는 원을 아래와 같이 그릴 수 있다. 여기서 선분(segment) uvuv의 수직이등분선과 선분(segment) vwvw의 수직이등분선을 그려보자. 세 점이 같은 직선위의 점이 아니므로 각 수직이등분선은 반드시 만날것이다. 만약 이 교점을 z0z_0이라 하면, z0z_0을 중심으로 하고 ww를 지나는 원은 세점을 지나는 유일한 클레인(cline)이 될 것이다.

Theorem 3.2.6

원에서 반전(inversion)변환은 클레인을 클레인으로 매핑한다. 특히 만약 클레인이 반전(inversion)변환된 원의 중심을 지난다면, 해당 클레인은 직선으로 사상(image)될 것이고 그렇지 않다면 원으로 사상될 것이다.

Proof.

만약 두 클레인이 직각(right angle)으로 교차한다면 이를 직교(orthogonal)한다고 한다. 예를들어, 어떤 직선이 원에 수직하다(orthogonal)하다는 명제의 필요충분조건은 직선이 원의 중심을 지난다이다(교점의 접선과의 직선의 각을 잰다). CC에서의 반전(inversion)의 중요한 특징 중 하나는 CC에 수직한(orthogonal)한 클레인은 그들 스스로 반전(inversion)된 것과 같다는 것이다. 이에 대한 증명은 생략한다.

Lemma 3.2.7

반지름이 rr이고 중심이 oo인 원 CC가 있고 pp가 원 CC 밖에 있는 점이라고 하자. 이 때 s=∣p−o∣s=|p-o|라 하자. 만약 pp를 지나고 원 CC와 mm과 nn에서 만나는 어떤 직선에 대해 아래 식이 성립한다.
∣p−m∣⋅∣p−n∣=s2−r2|p-m|\cdot|p-n|=s^2-r^2

Proof.

Theorem 3.2.8

원 CC가 중심이 z0z_0고 CC위의 점이 아닌 zz가 z≠z0z\neq z_0이 성립한다고 하자. zz를 지나는 어떤 클레인이 CC에 수직하다(orthogonal)는것과 클레인이 CC에서 zz의 대칭점 z∗z^*를 지난다는 것은 필요충분조건이다.

Proof.

Corollary 3.2.9

CC에 대한 반전(inversion)변환은 클레인(cline)이 CC에 대해 스스로 직교(orthogonal)하도록 변환한다.

Theorem 3.2.10

클레인(cline)에서 반전(inversion)변환을 해도 각의 크기(angle magnitude)는 보존된다.

Theorem 3.2.12 Inversion preserves symmetry points

iCi_C를 클레인(cline) CC에서 반전(inversion)변환이라 하자. 만약 pp와 qq가 클레인 DD에 대해 대칭관계(symmetric)라면 iC(p)i_C(p)와 iC(q)i_C(q) 또한 iC(D)i_C(D)에 대해 대칭관계이다.

Proof.

Theorem 3.2.14 Apollonian Circles Theorem

pp와 qq가 C\mathbb{C}에서 서로 다른 점이고 kk가 양의 실수라 하자. DD의 모든 점 zz가 C\mathbb{C} 위의 점이고 ∣z−p∣=k∣z−q∣|z-p|=k|z-q|를 만족하면 DD는 클레인(cline)이다.

Proof.

Theorem 3.2.16

교점이 없고 적어도 둘 중 하나는 원인 두 클레인(cline)이 있다고 하자. 이 때 두 클레인에 대칭( symmetric)인 두 점 pp와 qq가 반드시 존재한다.

Proof.