///
Search
📄

3.1 Basic Transformations of Complex

복소공간 C\mathbb{C}위에서 변환(transformation)의 기반이 되는 내용들을 살펴본다.

Definition

•
집합 AA와 BB가 주어졌을 때 함수 f:A→Bf:A\rightarrow B가 a1≠a2a_1\neq a_2일 때 f(a1)≠f(a2)f(a_1)\neq f(a_2)을 만족하면 일대일(surjective;one-to-one;1-1)이라고 한다. 여기서 a1,a2∈A,  f(a1),f(a2)∈Ba_1,a_2 \in A,\;f(a_1),f(a_2)\in B이다.
•
집합 A와 B가 주어졌을 때 함수 f:A→Bf:A\rightarrow B가 임의의 b∈Bb\in B에 대해 f(a)=bf(a)=b를 만족하는 a∈Aa\in A가 존재하면 대응(injective;onto)이라고 한다.
•
집합 AA의 함수 T:A→AT:A\rightarrow A가 일대일 대응(bijective: surjective + injective)함수면 변환(transformation)이라고 한다.
집합 AA의 변환 TT는 역변환 T−1T^{-1}을 가지며 ∀a∈A^\forall a\in A에 대해 T−1∘T(a)=aT^{-1}\circ T(a)=a이고 T∘T−1(a)=aT\circ T^{-1}(a)=a를 만족한다. 역함수 T−1T^{-1}는 [또한 집합 A의 변환(transformation)이 된다.

Basic Transformations of C\mathbb{C}

•
일반선형변환(general linear transformation): T(z)=az+bT(z)=az+b (a,b∈Ca,b \in \mathbb{C}이고 a≠0a\neq 0)
•
일반선형변환의 특별한 형태들
◦
이동(translation; bb): Tb(z)=z+bT_b(z)=z+b
◦
00기준 회전(rotation; θ\theta): Rθ(z)=eiθzR_{\theta}(z)=e^{i\theta}z
◦
z0z_0기준 회전(rotation; θ\theta): R(z)=eiθ(z−z0)+z0R(z)=e^{i\theta}(z-z_0)+z_0
◦
팩터(factor) k>0k>0에 대한 확대(dilation): T(z)=kzT(z)=kz
•
직선 LL에 대한 리플렉션(reflection): rL(z)=eiθzˉ+br_L(z)=e^{i\theta}\bar{z}+b (b∈Cb \in \mathbb{C}, θ∈R\theta \in \mathbb{R})

example 3.1.2 Translation

복소수 bb에 대해 함수 Tb:C→CT_b:\mathbb{C}\rightarrow \mathbb{C}가 아래와 같이 정의됬다고 하자.
Tb(z)=z+bT_b(z)=z+b
TbT_b를 이동(translation)라 하며 변환(transformation)이다.

Proof.

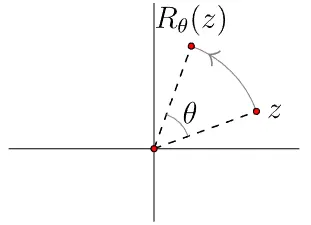
example 3.1.3 Rotation about the origin

θ\theta를 각(angle)이라 하면 Rθ:C→CR_{\theta}:\mathbb{C}\rightarrow \mathbb{C}로 정의되고 Rθ(z)=eiθzR_{\theta}(z)=e^{i\theta}z이다.
위 변환은 평면위의 점을 원점(origin)에 대해 각 θ\theta만큼 회전시킨다(θ>0\theta >0은 반시계방향이고 θ<0\theta < 0이면 시계방향이다). 이러한 경우를 보기위해 z=reiβz=re^{i\beta}라 하고 아래와 같이 쓸 수 있다.
Rθ(z)=eiθreiβ=rei(θ+β)R_{\theta}(z)=e^{i\theta}re^{i\beta}=re^{i(\theta+\beta)}

example 3.1.4 Rotation about any point

임의의 점 z0z_0에 대해 각(angle) θ\theta의 회전을 하기 위해선 세가지 단계를 거친다. 먼저 평면을 옮겨 z0z_0이 원점이 되도록 한다. 이 과정은 이동(translation) T−z0T_{-z_0}함수를 사용한다. 다음 각 점을 θ\theta만큼 원점에 대해 회전한다(RθR_{\theta}). 마지막으로 모든 점을 다시 이동시킨다(Tz0T_{z_0}). 이 변환과정은 아래와 같이 정리할 수 있다.
z⟼T−z0z−z0⟼Rθeiθ(z−z0)⟼Tz0eiθ(z−z0)+z0z\overset{T_{-z_0}}{\longmapsto}z-z_0 \overset{R_{\theta}}{\longmapsto} e^{i\theta}(z-z_0)\overset{T_{z_0}}{\longmapsto} e^{i\theta}(z-z_0)+z_0
다시말하면 회전 RR은 합성함수 Tz0∘Rθ∘T−z0T_{z_0}\circ R_{\theta} \circ T_{-z_0}이고 아래와 같은 함수로 정리할 수 있다.
R(z)=eiθ(z−z0)+z0R(z)=e^{i\theta}(z-z_0)+z_0

Theorem 3.1.5

만약 함수 TT와 SS가 집합 AA의 변환이라면 합성함수 S∘TS\circ T 또한 집합 AA의 변환이다.

Proof.

example 3.1.6 Dilation

실수 k>0k>0일 때 변환(transformation) T(z)=kzT(z)=kz를 확장(dilation)이라고 한다. 이 함수는 kk의 값에 따라 평면 위의 점의 위치를 원점기준으로 늘리거나 줄인다.
만약 z=x+yiz=x+yi라면 T(z)=kx+kyiT(z)=kx+kyi이고 zz와 T(z)T(z)는 둘 다 원점을 지나는 직선위의 점이다. 만약 k>1k>1이면 TT는 원점과 멀어지는 방향으로 팽창시키는 함수가 되고 0<k<10<k<1이면 원점과 가까운방향으로 축소시키는 함수가 된다. 수학에선 팽창과 축소를 구분하지 않고 확장함수(dilation function)라고 표현한다.

example 3.1.7 General Linear Transformations

T(z)=az+bT(z)=az+b이고 a,b∈Ca,b\in \mathbb{C}이고 a≠0a\neq0인 함수를 일반선형변환(general linear transformation)이라 한다. 함수 TT가 C\mathbb{C}에서의 변환(transformation)임을 보인다.

Proof.

Definition 3.1.8

T:A→AT:A\rightarrow A가 변환(transformation)이고 DD가 AA의 부분집합(subset)이라고 하자. 부분집합 DD의 상(image)은 T(D)T(D)라고 표기하고 x∈Dx\in D에 대한 모든 점 T(x)T(x)로 구성된다.
다시 말하면 아래와 같이 정리된다.
T(D)={a∈A∣a=T(x)  for  some  x∈D}T(D)=\{a\in A | a=T(x)\;for\;some\;x\in D\}
가령 LL이 직선(line)이고 TbT_b가 bb만큼 이동시키는 함수일 때,T(L) T(L) 또한 직선이 된다. 만약 평면 위의 직선이 이동한다면 그 또한 직선의 모양을 유지할 것이다. 사실, 직선(line)은 원(circle)과 같이 어떤 일반선형변환(general linear transformation)을 적용해도 유지된다. 이를 아래 Theorem을 통해 확인해보자.

Theorem 3.1.9

TT가 일반선형변환(general linear transformation)이라고 하면
1.
TT는 직선(line)을 직선(line)으로 매핑한다.
2.
TT는 원(circle)을 원(circle)로 매핑한다.

Proof.

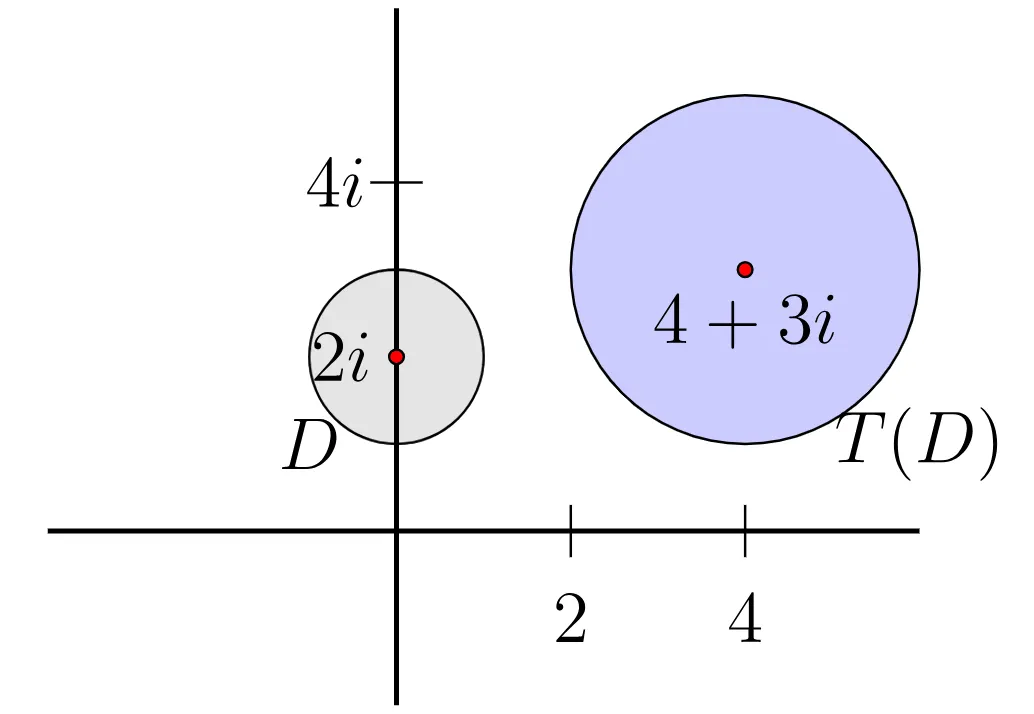
example 3.1.10. The image of a disk

원판(disk) D={z∈C∣  ∣z−2i∣≤1}D=\{z \in \mathbb{C}|\;|z-2i|\le 1\}가 있고 함수 T:C→CT:\mathbb{C}\rightarrow \mathbb{C}가 T(z)=2z+(4−i)T(z)=2z+(4-i)로 정의하자. 이 때 원판 T(D)T(D)는 4+3i4+3i를 중심으로 하고 반지름이 22인 원판(disk)이 되고 아래그림과 같다.
다음은 스무스 곡선(smooth curve) 사이의 각(angle)들을 보존하는 변환(transformation)에 대해 살펴본다. 평면곡선(planar curve)는 실수구간(real number interval)을 평면(plane)으로 매핑하는 함수 r:[a,b]→Cr:[a,b]\rightarrow \mathbb{C}를 말한다. 미분(derivative)값이 존재하고 모든 점이 00이 아닌 곡선(curve)을 스무스(smooth)라고 한다. r1r_1과 r2r_2가 한 점에서 접하는 복소공간 C\mathbb{C} 위의 스무스 곡선(smooth curve)이라고 하자. 곡선(curve) r1,r2r_1, r_2 사이의 각도(angle)는 ∠(r1,r2)\angle(r_1,r_2)라 표기하고 교점(point of intersection)에서 접선(tangent line)들 사이의 각으로 계산한다.

Definition 3.1.11

만약 z0z_0에서 만나는 모든 스무스 곡선(smooth curves) r1r_1과 r2r_2에서 ∠(r1,r2)=∠(T(r1,T(r2))\angle(r_1,r_2)=\angle(T(r_1,T(r_2))를 만족하면 C\mathbb{C}에서의 변환(transformation) TT는 점 z0z_0에서 각을 유지한다(preserves angles at point z0z_0)고 한다.
C\mathbb{C}에서의 변환(transformation) TT가 C\mathbb{C}의 모든 점을 변환해도 각이 유지되면 이때 각이 유지된다(preserves angles)라고 한다.
한 점에서 만나는 모든 스무스 곡선(smooth curve) r1r_1과 r2r_2가 ∣∠(r1,r2)∣=∣∠(T(r1,T(r2))∣|\angle(r_1,r_2)|=|\angle(T(r_1,T(r_2))|을 만족하면 C\mathbb{C}의 모든 점에 대해 C\mathbb{C}에서의 변환(transformation) TT가 각의 크기를 유지한다(preserves angle magnitudes)라고 한다.

Theorem 3.1.12

일반선형변환(general linear transformation)은 각을 유지한다(preserve angles).

Proof.

Definition 3.1.13

변환 T:A→AT:A\rightarrow A에서 T(a)=aT(a)=a를 만족하는 a∈Aa\in A를 변환 TT에서의 고정점(fixed point)이라고 한다.
변환(transformation)을 해도 그대로 유지되는 점을 고정점이라고 한다. 만약 b≠0b\neq0이라면 C\mathbb{C}에서의 변환 TbT_b는 고정점(fixed point)를 갖지 않는다(Tb(z)=z+bT_b(z)=z+b이므로 b≠0b\neq 0이라면 a+b=aa+b=a를 만족하는 aa가 있을 수 없다). 회전(rotation)과 확장(dilation)은 한 개의 고정점(fixed point)을 가지며 일반선형변환(general linear transformation) T(z)=az+bT(z)=az+b은 a≠1a\neq 1일 때 한개의 고정점(fixed point)를 갖는다. 고정점(fixed point)를 찾기 위해선 zz에 대해 아래의 수식을 해결해야 한다.
z=az+bz=az+b
예를들어 변환(transformation) T(z)=2z+(4−i)T(z)=2z+(4-i)에 대한 고정점을 찾기위해선 z=2z+(4−i)z=2z+(4-i)를 만족하는 z를 찾아야 하므로 z=−4+iz=-4+i가 된다. 따라서 T(z)=2z+(4−i)T(z)=2z+(4-i)가 원판(disk) DD를 T(D)T(D)로 이동시킬 때 −4+i-4+i에 해당하는 점들(points)은 움직이지 않는다.

Definition 3.1.14

∀z,w∈C^\forall z,w\in \mathbb{C}에 대해 CC에서의 변환 TT가 ∣T(z)−T(w)∣=∣z−w∣|T(z)-T(w)|=|z-w|를 만족하면 이를 유클리디안 아이소메트리(euclidean isometry)라고 한다.
유클리디안 아이소메트리(euclidean isometry)는 두 점 사이의 유클리드 거리(euclidean distance)를 유지한다.

example 3.1.15 Some Euclidean isometries of C\mathbb{C}

이동(translation)과 회전(rotation)은 유클리디안 아이소메트리(euclidean isometry)하다. 일반선형변환(general linear transformation) T(z)=az+bT(z)=az+b는 ∣a∣=1|a|=1일 때 유클리디안 아이소메트리(euclidean isometry)하다.
∣T(z)−T(w)∣=∣az+b−(aw+b)∣=∣a(z−w)∣=∣a∣∣z−w∣\begin{align*} |T(z)-T(w)|&=|az+b-(aw+b)| \\ &= |a(z-w)| \\ &=|a||z-w| \\ \end{align*}
∴∣T(z)−T(w)∣=∣z−w∣⟺∣a∣=1\therefore|T(z)-T(w)|=|z-w|\Longleftrightarrow |a|=1

example 3.1.16 Reflection about a line

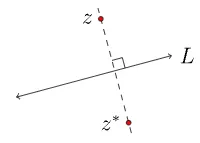
다음과 같이 정의되는 C\mathbb{C}에서의 변환(transformation)을 직선 LL에 대한 반사(reflection about a line LL)이라고 한다.
LL위의 점은 자기 자신으로 가고, LL 위에 없는 점 zz는 직선 LL이 zz∗zz^*의 수직이등분(perpendicular bisector)선이 되도록 z∗z^*로 이동한다.
LL에 대한 반사(reflection)는 대수적으로 아래와 같이 표현할 수 있다. 만약 직선 LL이 실수축이라면 아래 식과 같이 반사함수는 켤레함수와 같아진다.
rL(z)=zˉr_L(z)=\bar{z}
복소공간에서 직선 LL에 대해 반사(reflection)함수의 공식은 직선을 실수축에 대해 회전(rotation)과 이동(translation) 통해 변환하고 켤레를 취한 후 회전과 이동을 반대로 변환하면 만들 수 있다.
예를들어 직선 y=x+5y=x+5에 대한 반사(reflection)는 먼저 −5i-5i 만큼 수직으로 이동(translate)하고 −π4-\frac{\pi}{4}만큼 회전하고 실수축에 대칭한 후 π4\frac{\pi}{4}만큼 회전한 후에 마지막으로 5i5i만큼 이동(translate)한다. 정리하면 아래와 같다.
z↦z−5i↦e−π4i(z−5i)↦e−π4i(z−5i)‾=eπ4i(zˉ+5i)↦eπ4i⋅eπ4i(zˉ+5i)=eπ2i(zˉ+5i)↦eπ2i(zˉ+5i)+5i\begin{align*} z&\mapsto z-5i \\ &\mapsto e^{-\frac{\pi}{4}i}(z-5i) \\ &\mapsto\overline{e^{-\frac{\pi}{4}i}(z-5i)}=e^{\frac{\pi}{4}i}(\bar{z}+5i) \\ &\mapsto e^{\frac{\pi}{4}i}\cdot e^{\frac{\pi}{4}i}(\bar{z}+5i)=e^{\frac{\pi}{2}i}(\bar{z}+5i) \\ &\mapsto e^{\frac{\pi}{2}i}(\bar{z}+5i)+5i \end{align*}
eπ2ie^{\frac{\pi}{2}i}을 계산하기 위해 오일러 공식을 활용한다. eiϕ=cos⁡ϕ+isin⁡ϕe^{i\phi} = \cos{\phi}+i\sin{\phi}이고 ϕ\phi에 π2\frac{\pi}{2}를 대입하고 정리하면 아래와 같다.
eπ2i=cos⁡(π2)+isin⁡(π2)=0+i(1)=i\begin{align*} e^{\frac{\pi}{2}i}&=\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2}) \\ &=0 + i(1) \\ &=i \end{align*}
따라서 L:y=x+5L:y=x+5에 대한 대칭(reflection)을 정리하면 아래와 같다.
rL(z)=izˉ−5+5ir_L(z)=i\bar{z}-5+5i
식을 일반화 시켜 C\mathbb{C}위의 임의의 직선 LL에 대한 공식은 아래와 같다.
rL(z)=eiθzˉ+br_L(z)=e^{i\theta}\bar{z}+b
반사(reflection)은 회전(rotation)이나 이동(translation)보다 좀 더 기본형에 가까운 변환이다.

Theorem 3.1.17

•
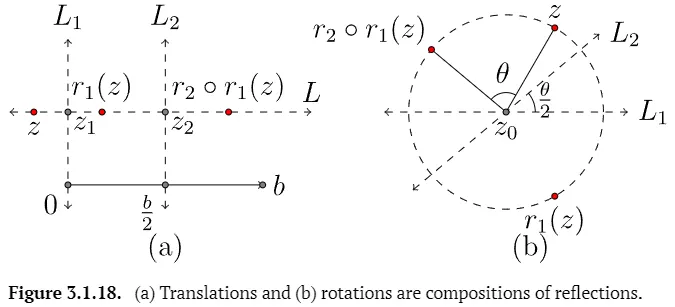
C\mathbb{C}에서 이동(translation)함수는 두 평행선에 대한 반사(reflection)함수의 합성함수다.
•
C\mathbb{C}에서 점 z0z_0에 대한 회전(rotation)함수는 z0z_0에서 교차하는 두 선에 대한 반사(reflection)함수의 합성함수다.

Theorem 3.1.19

직선 LL에 대한 반사(reflection about a line LL)는 유클리디안 아이소메트리(euclidean isometry)다. 또한 모든 반사(reflection)는 직선(line)을 직선으로, 원(circle)을 원으로, 그리고 각 크기 또한 보존한다.

Theorem 3.1.20

모든 유클리디안 아이소메트리(euclidean isometry)는 적어도 3개의 반사(reflection)의 합성으로 구성된다.