Search
📄

Cyclic Groups

💡
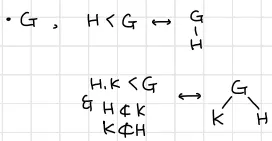
본 페이지에선 시클릭그룹(cyclic group)을 다룹니다. 그룹 GG의 원소 aa가 G={an  ∣  n∈Z}G=\{a^n \;|\; n \in Z\}가 존재하면 그룹 GG를 시클릭 그룹(cyclic group; 순환군)이라 합니다. 또한 원소 aa로 만들어지는 GG는 G=⟨a⟩G=\langle a \rangle라 표기합니다.
rmk u(10)={1,3,7,9}={30,31,32,33}=⟨3⟩u(10)=\{1,3,7,9\}=\{3^0,3^1,3^2,3^3\}=\langle 3 \rangle
u(n)u(n)은 항상 시클릭그룹일까? No! 반례로 u(8)={1,3,5,7}u(8)=\{1,3,5,7\}을 살펴본다.
⟨1⟩={1}⟨3⟩={3,1}⟨5⟩={5,1}⟨7⟩={7,1}\begin{matrix} \langle 1 \rangle = \{1\} \\ \langle 3 \rangle = \{3,1\} \\ \langle 5 \rangle = \{5,1\} \\ \langle 7 \rangle = \{7,1\} \\ \end{matrix}
u(8)=⟨a⟩u(8)=\langle a \rangle을 만족하는 a∈u(8)a\in u(8)이 존재하지 않으므로 시클릭그룹이 아니다.

Subgroup Lattice

그룹의 다양한 서브그룹(subgroup)들의 관계를 표현하기 위해 서브그룹 사다리(Subgroup Lattice)를 활용할 수 있다.

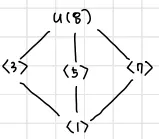
Example

Subgroup lattice of u(8)u(8)

Theorem

a∈Ga \in G
1.
if ∣a∣=∞  ⇒  [ai=aj    ⇔    i=j]|a|=\infty \; \Rightarrow \; [a^i=a^j \;\;\Leftrightarrow \;\; i=j]
2.
if ∣a∣=n<∞,|a|=n<\infty,
a.
⟨a⟩={e,a,a2,⋯ ,an−1}\langle a \rangle = \{ e, a, a^2, \cdots, a^{n-1}\}
b.
ai=aj⇔n∣(i−j)    (⇔i≡nj)a^i=a^j \Leftrightarrow n|(i-j)\;\; (\Leftrightarrow i \underset{n}{\equiv} j)

proof

Cor 1

For a∈Ga\in G, ∣a∣=∣⟨a⟩∣|a|=|\langle a \rangle|

Cor 2

Assume ∣a∣=n|a|=n if ak=e⇒n∣ka^k=e \Rightarrow n|k