///
Search
📄

3.3 The Extended Plane

∣z−z0∣=r|z-z_0|=r로 주어진 원 CC에 대한 반전(inversion)변환에 대해 고려해보면 z0z_0에 가까운 점은 z0z_0로 부터 가장 먼 평면위의 점으로 매핑된다. 사실, 리미트(limit)가 z0z_0인 CC위의 연속점들은 크기가 ∞\infty로 가까워지는 점들로 반전변환된다. 역으로 크기가 ∞\infty로 가는 점들은 리미트가 z0z_0인 점들로 반전되게 된다.
이를 염두에 두고 무한원점(the point at infinity)을 정의하고 ∞\infty라 표기한다. 또한 이 새로운점을 평면에 연결하여 C∞\mathbb{C}^{\infty}라 하는 확장평면(extended plane)을 얻는다. 그 후, z0z_0와 ∞\infty를 포함하도록 원 CC에서 반전변환을 확장할 수 있다. 특히, 중심이 z0z_0이고 반지름이 rr인 원 CC에서 C+\mathbb{C}^+의 반전변환 iC:C+→C+i_C:\mathbb{C}^+\rightarrow \mathbb{C}^+는 아래와 같다.
iC(z)={r2(z−z0)ˉ+z0if  z≠z0,∞;∞if  z=z0;z0if  z=∞i_C(z)= \begin{cases} \frac{r^2}{\bar{(z-z_0)}}+z_0 &\mathtt{if}\;z\neq z_0,\infty;\\ \infty &\mathtt{if}\;z=z_0;\\ z_0 &\mathtt{if}\;z=\infty \end{cases}
확장평면의 반전변환에 대해 z0z_0과 ∞\infty는 원의 반전에 대해 대칭점으로 정의할 수 있다.
공간 C+\mathbb{C}^+는 본 책의 모든 기하에서 사전정의된 공간이며 ∞\infty를 고려해야할 어떤 점으로 생각해야한다. 모든 평행이동, 팽창, 그리고 회전은 점 ∞\infty를 포함하도록 재정의 된다.
그렇다면 C+\mathbb{C}^+에서 ∞\infty는 어디있을까? ∞\infty는 복소평면에서 어떤 선의 방향에 따라 진행하는 것으로 접근할 수 있다. 더 일반적으로, 만약 {zn}\{z_n\}이 n→∞n\to \infty에 대해 ∣zn∣→∞|z_n|\to \infty인 복소수열이라 하면 lim⁡n→∞zn=∞\lim_{n\to\infty}z_n=\infty라 할 수 있다.
우린 ∞\infty를 확장평면에서 모든 선 위에 있다고 추정하며 임의의 선에 대해 반사시키면 ∞\infty로 고정된다.

Theorem 3.3.1

도메인 C+\mathbb{C}^+에 확장되는 임의의 선형변환은 ∞\infty를 고정한다.

Proof.

따라서 새로운 도메인 C+\mathbb{C}^+에서 기본변환을 위한 고정점(fixed point)를 수정한다.
•
C+\mathbb{C}^+의 평행이동 TbT_b는 한 점(∞\infty)으로 고정된다.
•
C+\mathbb{C}^+의 원점 RθR_{\theta}에 대한 회전변환은 두 점으로 고정된다(00과 ∞\infty)
•
C+\mathbb{C}^+의 확장변환 T(z)=kzT(z)=kz은 두 점으로 고정된다(00과 ∞\infty)
•
직선 LL에 대한 C+\mathbb{C}^+의 반사변환 rL(z)r_L(z)은 LL 위의 모든 점으로 고정된다(이제 ∞\infty를 포함한다).

Example 3.3.2 Some transformations not fixing ∞\infty.

C+\mathbb{C}^+에서 아래 변환은 ∞\infty를 고정하지 않는다.
T(z)=i+1z+2iT(z)=\frac{i+1}{z+2i}
TT가 ∞\infty로 보내는 점과 TT가 ∞\infty를 어디로 보내는지 확인한다. 먼저 ∞\infty로 보내는 점은 분모를 0으로 보내야하므로 T(−2i)=∞T(-2i)=\infty가 된다. T(∞)T(\infty)는 분모가 ∞\infty로 가므로 T(∞)=0T(\infty)=0이 된다.
만약 T(z)가 아래와 같다면,
T(z)=iz+(3i+1)2iz+1T(z)=\frac{iz+(3i+1)}{2iz+1}
T(i/2)=∞T(i/2)=\infty이고 T(∞)=1/2T(\infty)=1/2이다.
이전 챕터에서 살펴본 C+\mathbb{C}^+의 확장에 대한 몇가지 결과를 다시 확인한다.
•
C+\mathbb{C}^+에서 서로 다른 임의의 세개의 점을 지나는 클레인은 유일하게 존재한다
•
클레인에 대해 반전변환(inversion)은 C+\mathbb{C}^+ 의 모든 점들의 각도의 크기를 보존한다.
•
반전변환은 C+\mathbb{C}^+위의 모든 대칭점을 유지한다.
•
Theorem 3.2.16는 이제 동심원을 포함하여 교차하지 않는 모든 경사면에 적용된다. 두 원이 동심원이면 두 원 모두에 대칭인 점은 ∞\infty이고 동일한 중심을 가진다.

스테레오 사영(Stereographic Projection)

Definition 3.3.3

unit 2-sphere는 S2\mathbb{S}^2라 하고 3차원 공간에서 원점으로부터 1만큼 떨어진 모든 원들의 집합이다.
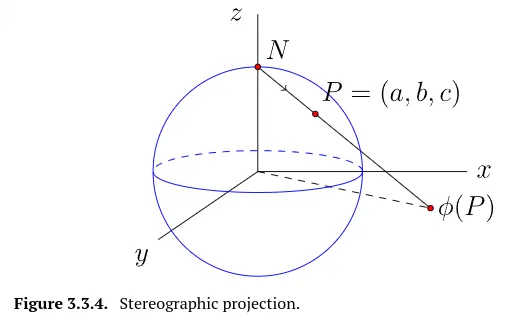
S2={(a,b,c)∈R3  ∣  a2+b2+c2=1}\mathbb{S}^2=\{(a,b,c)\in\mathbb{R}^3\;|\;a^2+b^2+c^2=1\}
unit 2-sphere는 보통 간단하게 “구(sphere)”라고 부른다. 확장평면에 대응(onto)되는 구의 스테레오 사영(Stereographic projection)은 아래와 같이 정의된다. 구의 북쪽 축을 N=(0,0,1)N=(0,0,1)이라 하자. 구 위의 모든 점 P≠NP\neq N에 대해 ϕ(P)\phi(P)는 xyxy평면에 있는 직선 NP→\overrightarrow{NP} 위의 점이다.
스테레오 사영(Stereographic projection)은 대수적으로 표현할 수 있다. N=(0,0,1)N=(0,0,1)과 P=(a,b,c)P=(a,b,c)를 지나는 직선은 방향벡터 NP→=⟨a,b,c−1⟩\overrightarrow{NP}=\langle a,b,c-1\rangle로 표현하고 아래와 같은 방정식으로 표현할 수 있다.
r⃗(t)=⟨0,0,1⟩+t⟨a,b,c−1⟩\vec{r}(t)=\langle 0,0,1 \rangle+t\langle a,b,c-1\rangle
xyxy평면과 직선의 교점은 zz가 00일때 이다. 이는 t=11−ct=\frac{1}{1-c}일 때 (a1−c,b1−c,0)\big( \frac{a}{1-c},\frac{b}{1-c},0\big)에 대응되는 점이다.
따라서 c≠1c\neq 1인 구 위의 점 (a,b,c)(a,b,c)에 대한 스테레오 사영 ϕ:S2↦C+\phi:\mathbb{S}^2 \mapsto \mathbb{C}^+는 아래와 같다.
ϕ((a,b,c))=a1−c+b1−ci\phi((a,b,c))=\frac{a}{1-c}+\frac{b}{1-c}i
이에 따라 ϕ\phi는 NN을 ∞\infty로 보낸다. 또한 NN에 가까워지는 S\mathbb{S} 위의 연속점들은 크기가 ∞\infty에 가까워지는 C\mathbb{C}의 투영점(image)이 될 것이다.

∞\infty에서 각도(angles)

만약 ∞\infty를 단순히 C+\mathbb{C}^+위의 또다른 점이라고 하면 우리는 해당 점에서의 각도에 대해 논할 수 있다. 가령 ∞\infty에 임의의 두 직선의 교점이 있다면 ∞\infty에서 교점의 각도에 대한 질문이 있을 수 있다. 우리는 해당 질문에 대한 답을 다음의 정리에 의하여 스테레오 사영을 통해 해결할 수 있다.

Theorem 3.3.5

스테레오 사영은 각도를 보존한다. 만약 구 위에 있는 두 곡선이 각도 θ\theta로 교차하면 이들이 C+\mathbb{C}^+에 사영되도 교점의 각도는 θ\theta이다.
따라서 C+\mathbb{C}^+에 있고 ∞\infty에서 교차하는 두 곡선의 각도는 스테레오 사영 연산에 대한 프리이미지(pre-image)에서 각도와 같다. ∞\infty에서 두 평행직선의 각도는 0이다. 또한 만약 두 직선이 유한점 pp 뿐만 아니라∞\infty 에서도 교차한다면 ∞\infty에서 교차하는 각도는 pp에서 교점의 각도의 음의각도(negative)와 같다. 결론적으로 원에 대한 반전변환은 C+\mathbb{C}^+ 위의 모든 점에 대해 각도의 크기를 보존한다.