///
Search
📄

3.5 Möbius Transformations: A Closer Look

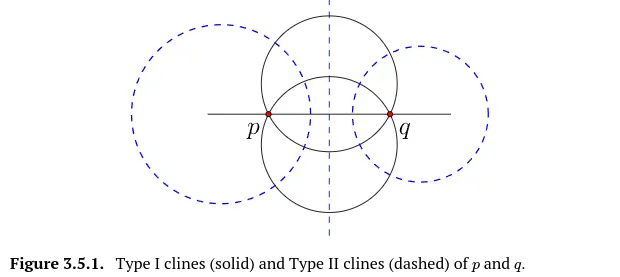
두 점 p,q∈C+p,q\in \mathbb{C}^+가 주어졌을 때 pp,qq의 타입-I 클레인은 pp와 qq를 지나는 클레인이고 pp,qq의 타입-II 클레인은 pp와 qq를 대칭으로 하는 클레인을 말한다. 아래 그림에서 실선은 pp,qq의 타입-I 클레인이고 점선은 타입-II 클레인이다.
Theorem 3.2.8 에 의해 pp,qq의 임의의 타입-I 클레인과 타입-II 클레인은 서로 직각이다. 게다가 뫼비우스 변환이 클레인과 대칭점을 보존하기 때문에 뫼비우스 변환이 타입-I 클레인과 타입-II 클레인을 모두 보존한다. 특히 만약 CC가 pp,qq의 임의의 타입-I이라면 T(C)T(C)는 T(P)T(P)와 T(q)T(q)의 타입-I 클레인이다. 유사하게 만약 CC가 pp,qq의 임의의 타입-II이라면 T(C)T(C)는 T(P)T(P)와 T(q)T(q)의 타입-II 클레인이다. 우리는 이런 성질을 활용할 것이다.
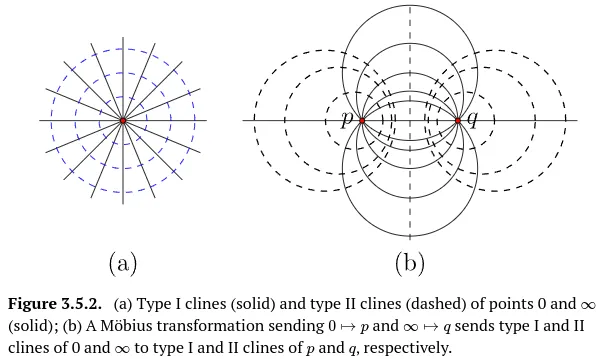
예를들어 00과 ∞\infty의 타입-I 클레인은 원점을 지나가는 직선이고 점 00과 ∞\infty의 타입-II 클레인은 원점이 중심인 원이다(원의 반전변환은 원의 중심을 ∞\infty로 보낸다). 이 경우에 타입-I 클레인은 타입-II 클레인에 수직이고 이들은 아래 그림 (a)와 같이 평면의 좌표계(극 좌표계)를 만들기 위해 결합한다.
우린 (b)와 같이 클레인을 p,q≠∞p,q\neq \infty일 때 0↦p,∞↦q0\mapsto p, \infty\mapsto q인 뫼비우스 변환으로 옮길 수 있다. 원점을 지나는 직선은 pp,qq의 타입-II 클레인에 매핑되고 원점을 중심으로 하는 원은 pp,qq의 타입-II 클레인으로 매핑된다. 이 결과는 평면에서 일반적인 좌표계를 보조하는 클레인 시스템이다. 각 평면위의 점 zz는 pp와qq의 타입-I과 타입-II의 교점에 있고 두 클레인은 직각으로 교차한다.

Example 3.5.3 00과 ∞\infty 고정

변환 TT가 서로 다른 두 점 pp와 qq(둘다 ∞\infty가 아님)을 고정하는 뫼비우스변환이라 하자.
S(z)=z−pz−qS(z)=\frac{z-p}{z-q}
를 p↦0,q↦∞p\mapsto 0, q\mapsto \infty인 뫼비우스 변환이라고 하자. 그리고 UU를 아래와 같은 합성함수 식으로 결정되는 뫼비우스 변환이라고 하자.
U=S∘T∘S−1\begin{align} U=S\circ T \circ S^{-1} \end{align}
이 때,
U(0)=S∘T∘S−1(0)=S∘T(p)=S(p)=0,U(0)=S\circ T\circ S^{-1}(0)=S\circ T(p)=S(p)=0,
U(∞)=S∘T∘S−1(∞)=S∘T(q)=S(q)=∞U(\infty)=S\circ T \circ S^{-1}(\infty)=S\circ T(q)=S(q)=\infty
가 성립한다.
즉, 뫼비우스 변환 UU는 00과 ∞\infty를 고정한다. 따라서 UU는 회전변환이거나 확장변환이거나 두 변환의 합성변환이다. 따라서 Example 3.5.3 0과 \infty 고정 에 의해 U(z)=reiθzU(z)=re^{i\theta}z로 표현할 수 있다.
(1)의 방정식을 이용하면 S∘T=U∘S S \circ T=U \circ S로 다시 쓸 수 있고 이를 이용하면 뫼비우스 변환의 정규형(normal form)이라 불리는 방정식을 이끌어낼 수 있다.

Definition. 두 고정점에 대한 정규형(Normal form, two fixed points)

서로 다른 고정점 pp와 qq에 대한(둘다 ∞\infty가 아닌) 뫼비우스 변환 TT의 정규형은 아래와 같다.
T(z)−pT(z)−q=reiθ⋅z−pz−q\frac{T(z)-p}{T(z)-q}=re^{i\theta}\cdot\frac{z-p}{z-q}
위 정규형은 aa,bb,cc,dd로 이뤄진 형식보다 더 많이 사용된다. pp와qq는 고정점이고 rr은 pp,qq의 타입-l 클레인에 대한 확장계수(dilation factor), θ\theta는 pp,qq의 타입-ll 클레인에 대한 회전계수(rotation factor)이다.
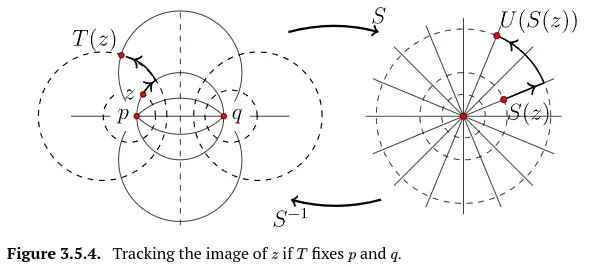
(1)의 방정식을 통해 T=S−1∘U∘ST=S^{-1}\circ U \circ S를 확인할 수 있다. 이러한 관점에선 TT는 세단계의 연산을 합성한 것이 된다. 어떤 어떤 점 zz가 아래 그림과 같이 pp,qq의 타입-Il 클레인과 pp,qq의 타입-l 클레인의 교집합을 통해 올라가고 있다고 하자.
먼저 zz는 SS를 통해 원점을 지나는 직선과 원점을 중심으로 하는 원 사이의 교점으로 이뤄지는 공간인 S(z)S(z)로 매핑된다. 둘째로 UU(U(z)=reiθzU(z)=re^{i\theta}z로 표현되는)는 S(z)S(z)를 원점을 지나는 직선을 따라 확장계수 rr에 의해 이동하여 원점을 중심으로 하는 새로운 원으로 보내고 원을 따라 회전계수 θ\theta만큼 이동하게 된다. 셋째로 S−1S^{-1}은 U(S(z))U(S(z))를 다시 pp,qq의 타입-Il 클레인과 pp,qq의 타입-l 클레인의 교집합 공간으로 보낸다. 이 점은 S−1(U(S(z)))S^{-1}(U(S(z)))이며 T(z)T(z)와 같다.
이를 통해 변환 TT가 점을 pp,qq의 타입-l 클레인을 따라서 확장계수 rr을 통해 이동시킨 후 회전계수 θ\theta를 통해 pp,qq의 타입-ll 클레인을 따라 이동시킨다는 것을 확인할 수 있다.
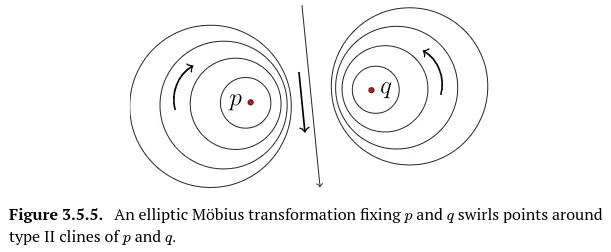
지금부턴 정규형의 특별한 두가지 경우를 확인한다. 만약 아래 그림과 같이 변환이 ∣reiθ∣=1|re^{i\theta}|=1로 확장이 없고 pp,qq의 타입-ll 클레인에 대해 단순히 회전한다고 하자. 이런 뫼비우스 변환을 타원 뫼비우스 변환(elliptic Möbius transformation)이라고 한다.
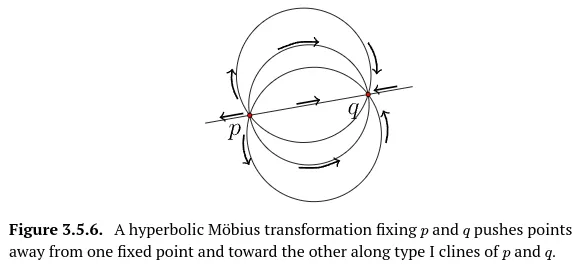
두번째 특별한 경우는 θ=0\theta=0일 때 이다. 확장 계수 rr이 있고 회전하지 않을 때 이다. 모든 점은 아래 그림과 같이 pp,qq의 타입-l을 따라 움직인다. 이런 뫼비우스 변환을 쌍곡 뫼비우스 변환(hyperbolic Möbius transformation)이라 한다. 쌍곡 뫼비우스 변환은 pp와 qq가 고정되고 모든 점을 pp에서 qq로 보내거나 또는 qq에서 pp로 보낸다.
이런 두가지 특별한 경우가 아니라면, TT는 단순히 이들 둘의 합성변환이 되고 이런 경우의 뫼비우스 변환을 로소드로믹(loxodromic)이라 한다.
만약 뫼비우스 변환 두개의 유한점(finite points) pp와 qq를 고정하고 항등변환이 아니라면, 어떤 유한점은 ∞\infty로 간다. 또한 ∞\infty는 유한점으로 변환된다. 무한점으로 가는 점을 변환의 극점(pole)이라고 하고 z∞z_{\infty}로 표기한다. 즉, T(z∞)=∞T(z_{\infty})=\infty이다. TT의 반전극점(inverse pole of T)는 ∞\infty의 사상(image)이고 w∞w_{\infty}로 표기한다. 즉, T(∞)=w∞T(\infty)=w_{\infty}이다. 네 점 pp,qq,z∞z_{\infty},w∞w_{\infty}는 간단한 관계를 가진다.

Lemma 3.5.7

뫼비우스 변환 TT가 서로 다른 두 점 pp와 qq를 고정하고 z∞→∞z_{\infty}\to \infty, ∞→w∞\infty \to w_{\infty}라 하자. 이 때 p+q=z∞+w∞p+q=z_{\infty}+w_{\infty}를 만족한다.

Proof.

Theorem 3.5.8

만약 뫼비우스 변환 TT가 서로다른 유한점 pp, qq를 고정하고 z∞→∞z_\infty\to\infty, ∞→w∞\infty\to w_\infty라면 아래 식을 만족한다.
T(z)=w∞z−pqz−z∞.T(z)=\frac{w_\infty z-pq}{z-z_\infty}.

Proof.